Authored by Mergen H Ghayesh,
Abstract
In this paper, a brief review is presented on the influence of nonlinearity on the mechanics of microscale structures. The constitutive equations of size-dependent elasticity-based theories such as the couple stress are presented. The linear size-dependent elasticity-based models of microscale structures are discussed. Furthermore, the effects of different types of nonlinearity on the static stability, oscillation and static deformation of microscale structures are reviewed.Keywords: Microstructures; Modified elasticity; Geometrical nonlinearity; Size effects
Introduction
The mechanical behaviour of microscale structures such as microscale beams and plates are highly nonlinear in many practical cases due to large applied forces as well as strong interactions between different parts at microscales. In applications such as resonators, sensors and generators, in which the mechanical behaviour plays a crucial role, understanding the nonlinear response becomes important [1-5]. In recent years, a number of size-dependent elasticity-based models have been used to analyze the static stability, time-dependent deformation and static deformation of the structural components of microscale and nanoscale systems [6-9]. The appropriate elasticity-based model is selected according to the size of the structural component. The couple stress and strain gradient theories as well as their modified versions are mainly utilised for structures at microscales [10-15]. However, the nonlocal elasticity-based models such as the pure nonlocal elasticity [16-23] and nonlocal strain gradient elasticity [24-28] are reasonable for nanoscale structures.Linear Analysis of Microscale Structures
To analyse the linear mechanics of microscale structures, modified couple stress models have extensively been employed. According to this theory, one can write [4,32].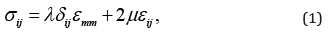

in which λ and μ are employed to represent the Lamé constants; γ is the size parameter; δij , mij and χij denote the Dirac delta function, deviatoric couple stress and symmetric curvature, respectively[33]. Equations (1) and (2) have extensively been utilised for examining the linear [15,34] and nonlinear [35- 37] mechanical behaviour of microscale structural components.
Stretching-Type Nonlinearity
In large deformations, due to the stretch of the middle surface of plates and the center line of tubes, the effects of nonlinear strains become significant. The effects of stretching-type nonlinearity on the mechanics of microstructures have been analyzed [10,36,38- 43]. Size-dependent models incorporating stretching-type nonlinearity have been developed for various microscale structures such as beams [39,44,45], plates [10,41,46] and shells [40,47]. For the formulation of mechanical behaviour, the couple stress model is used for structural components at microscales [11,35,36,48- 50]. More recently, an elasticity-based model with consideration of both strain gradient and nonlocal effects has been proposed for the large-amplitude dynamics of ultrasmall tubes incorporating the stretching-type nonlinearity [25,26,51].Curvature-Type Nonlinearity
For particular types of microscale structures such as microcantilevers, the curvature-type nonlinearity becomes important. Taking into account this type of geometrical nonlinearity in these systems yields a more reliable continuum model for investigating the static and dynamic responses. Size-dependent continuum models incorporating curvature-type nonlinearity have been developed for the large-amplitude vibration [52], dynamics [53,54], stability [55] and modal interaction [56] of ultra-small cantilevers. In addition, the effects of curvature-type nonlinearity on the nonlinear mechanics of functionally graded microcantilevers have lately been analyzed [56-58].Conclusion
A brief review was presented in this paper for the nonlinear analysis of microscale structural components including microscale beams and plates. It was concluded that for microscale beams with clamped-free boundary conditions (i.e. cantilevers), both types of geometrical nonlinearity are important while for microscale beams with pinned-pinned and clamped-clamped boundary conditions, the stretching-type nonlinearity is dominant. Although a few nonlinear models have been proposed for the large deformation of microscale structures, more investigation is required to better understand the effect of different types of nonlinearity on the mechanical behavior at microscale levels.To read more about this article... Open access Journal of Journal of Engineering Sciences
Please follow the URL to access more information about this article
https://irispublishers.com/gjes/fulltext/nonlinear-mechanics-of-microstructures.ID.000518.php
To know more about our Journals... Iris Publishers
To know about Open Access publisher





No comments:
Post a Comment