Iris Publishers- Open access Journal of Engineering Sciences | Darcy Convection Anisotropic Problem with Multi Stability of Stationary Motions for Rectangle

Authored by Abdelhafez MA



Based on the Darcy model, fluid convection in a porous rectangle is analyzed taking into account anisotropy of thermal characteristics and permeability. Relations between parameters for which the problem belongs to the class of co-sssymmetric systems are derived. For this case explicit formulas for the critical numbers of the loss of stability of mechanical equilibrium are found. Using a finite-difference method that preserves the cosymmetry of the problem, family of stationary convective regimes is computed. Through the computational experiment the destruction of families is demonstrated in the case of violation of the conditions of co-symmetry. As result the appearance of a finite number of stationary regimes are obtained.


The plane problem of heating a rectangular container is considered Ω = [0, a] × [0, b], on the boundary of which the conditions of impermeability and temperature pro le linear in height are given T∗(y) = T₂ − y(T₂ − T₁)/b, Where T₁ И T₂ temperature at the top (y = b) and bottom (y = 0) boundaries, respectively, the force of gravity acts in the direction opposite to the coordinate y. Next, a perturbation of the temperature field is introduced T (x, y, t) = T∗(y) + θ (x, y, t) and a transition is made to dimensionless quantities [1]. For stream function ψ and temperature deviations θ the following initial-boundary problem is obtained with respect to the linear profile:
Here t - time, μ_ij - the components of the tensor of dimensionless coefficients of reverse permeability, d_ij - coefficients thermal conductivity, λ - Rayleigh filtration number.
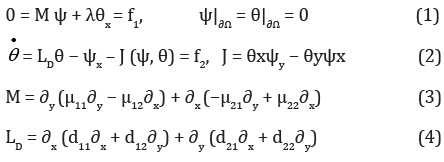
Equations (1)-(4) supplemented with initial conditions θ (x, y, 0) = θ0(0, y).
With μ₁₁ = μ₂₂ = d₁₁ = d₂₂ = 1 И μ₁₂ = μ₂₁ = d₁₂ = d₂₁ = 0 from (1)-(2) equations are obtained that correspond to the isotropic problem. In this case, the system of equations is co-symmetric according to [2], those there is a vector field L, which is orthogonal to the vector field of the problem and does not vanish on a nontrivial stationary solution. IN [1] set the conditions under which the task (1)-(4) is cosymmetric, these conditions are clarified by the following lemma.

Lemma

Under the conditions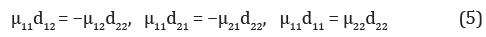
co-symmetry of the system (1)-(4) is a vector function L = (d₂₂θ ,−μ₁₁ψ

Mechanical Equilibrium Stability Analysis

Equations (1)-(4) satisfies zero solution θ = ψ = 0, corresponding to mechanical equilibrium. In the case of μ₁₂ = μ₂₁ = d₁₂ = d₂₁ = 0 from (1)-(4) for perturbations, a linear system is obtained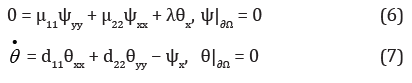
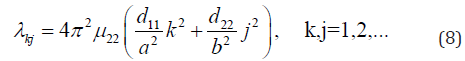
It turns out that critical Rayleigh numbers λ, corresponding to the monotonic instability of mechanical equilibrium, are given by the formula
The emergence of the instability of mechanical equilibrium corresponds to the eigenvalue λ₁₁. Critical values of the Rayleigh filtration number λ for isotropic case follow from (8) at μ₂₂ = d 11 = d₂₂ = 1. In [2] for the isotropic Darcy problem, it is shown that the first critical value λ₁₁ twice for an arbitrary region, and when the transition parameter λ through λ₁₁ from a state of mechanical equilibrium a family of stationary modes branches o (equilibria). The calculations performed in this paper showed that a similar scenario is realized for the Darcy anisotropic problem. The equilibrium family for the plane problem of filtration convection has a variable spectrum, this distinguishes the co-symmetric situation from the symmetric one. Every transition λ through subsequent critical values λ_kj corresponds to the bifurcation of the birth of a family of unstable stationary modes.
In case of violation of conditions (5) vector function L = (d₂₂θ, -μ₁₁ψ) is not a problem co-symmetry. In this case, instead of a oneparameter family, a finite number of convective regimes are formed. (stationary or non-stationary) [3-5].
Further numerical research is carried out for the case μ_ij = d_ij = 0, (i ≠ j). Following [3], it turns out selective (selection) function
Here ψ and θ are the solution to the problem (1)-(4) on condition μ₁₁d₁₁ = μ₂₂ d₂₂ (case of co-symmetry) belonging to the family of stationary modes. Parameter ν sets parametrization on the family, ν ∈ [0, 1]. symbols 'ii μ И 'ij d denoted parameter values that differ from those for which the family is calculated. At μ'_ii = μ'_ii , d'_ii = d'_ii , (i = 1, 2) selective function S(ν) = 0. If a μ'_ii ≠ μ'_ii and/ or d'_ii ≠ d'_ii , (i = 1, 2), then there are modes corresponding to the solutions of the equation S(ν) = 0. If one parameter is disturbed d’₁₁ = d₁₁ + ε selective equation (9) will take the following form

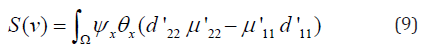
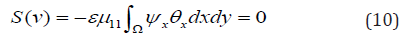
Numerical Study

In the case of anisotropy, the Darcy problem with co-symmetry in the [1] an analysis of the occurrence of stationary convective regimes, branching o from the loss of stability of mechanical equilibrium, is given. The conditions on the coefficients of the system under which the problem has co-symmetry and the branching of the continuous family of stationary modes are analytically determined. In this paper, the results of calculations of the families themselves are presented on the basis of the scheme [6], and the study of their destruction under violation of the conditions. Table 1 presents the results of calculations of the critical Rayleigh numbers depending on combinations of parameters of reverse permeability μii and thermal conductivity d₂₂ ΠpИ d₁₁ = 1, a = 2.5, b = 1. The value λ₁₁, λ21 is calculated by the formula (8), and the quantities λ^h₁ , λ^h₂ , λ^h₃ h meet the first three critical values on the grid 36 × 12. In the last column ⪡KOC⪢ notes the fulfillment of the conditions of co-symmetry (5).

To read more about this article...Open access Journal of Engineering Sciences


Please follow the URL to access more information about this article
https://irispublishers.com/gjes/fulltext/darcy-convection-anisotropic-problem-with-multi-stability-of-stationary-motions-for-rectangle.ID.000542.php

To know more about our Journals... Iris Publishers

To know about Open Access publisher