Iris Publishers- Open access Journal of Current Trends in Civil & Structural Engineering | Stability Performance Assessment of Pipelines under Hydrostatic Pressure

Authored by Tadeh Zirakian

Abstract

Pipelines are an economical means of transporting oil and gas. A commonly encountered performance issue with such structures, however, is their susceptibility to buckling under hydrostatic and hydrodynamic pressure loads. In such a failure scenario, the pipe will suddenly collapse under the action of the loads and can render the transport structure as ineffective. The engineering design of pipes must therefore account for the action and magnitudes of such anticipated service loading, referred to as buckle propagation pressure, in achieving an adequate and sound performance. As for the notion of economy, since buckle propagation pressure is closely related to the pipe wall thickness, it has a direct bearing on overall project costs. In this study, to simulate in situ conditions of subsea pipelines, only uniform hydrostatic pressure was taken into consideration as the source for loading. A finite element method (FEM) model was then used to examine the buckling modes on pipes of two different diameters varying at four diameter-to-thickness ratios. With the pipes modeled as having clamped supports, predicted values of stress, strain, reaction force, and displacement at the ends and at midspan, were obtained. The results found show an inverse relationship between the diameterto- thickness ratios and buckling capacities of the pipes.

Keywords:Pipeline; Buckling; Hydrostatic pressure; Diameter-to-thickness ratio; Numerical simulation

Introduction

Subsea pipelines are externally loaded by a constant source of hydrostatic pressure. Local buckling can occur at pressures much lower than that required for critical buckling (P_cr), and after one region has been compromised, the zone of damage may begin to expand along the length of the pipe leading to eventual collapse of the pipeline [1,2]. During buckling and the ensuing propagation of damage, significant changes are found to occur in the cross section of the pipe geometry. An analysis of post-buckling behavior prior to total collapse should be considered in order to better understand the gradual failure mechanisms of these structures in both the radial as well as longitudinal directions [3-6]. As depicted in Figure 1, the phenomenon of buckling tends to flatten the pipeline in cross section locally, while propagation of this damage longitudinally may be characterized by three zones: the near-end buckled and far-end unbuckled regions, and a transition of pipe length between the two (Figure 1). After buckling initiation, damage propagation reaches a steady state for which the external hydrostatic pressure is constant. Buckling propagation stops when the external hydrostatic pressure is lower than the buckle propagation pressure [7]. According to the elastic stability theory, deformation of pipeline occurs in two stages: pre-buckling and post-buckling [8]. Research has shown that in loads lower than the buckling load, deformation of pipeline is based on a stable pre-buckling path [9,10,12]. As pressure increases, the pipeline section starts to develop plastic hinges and then begins to fail. With the continual increase in pressure, the pipeline undergoes further deformation in the radial direction until the onset of pipeline buckling at a certain external pressure, i.e. the critical buckling load P_cr. Beyond this point, the pipeline behavior is described by the post-buckling path, which may be unstable for pipelines with elasto-plastic materials. The pipeline deformation diagram is portrayed in Figure 2 Illustrated in Figure 3 is also the development of yield lines with buckling propagation along the pipeline section (Figure 2 & 3).

Behavior of pipelines in response to external pressure has been the subject of numerous studies, which have shown that length of the pipe and ratio of its diameter to the wall thickness play a decisive role in the pipe’s resistance against buckling. According to Bresse [13], the stability of pipelines under hydrostatic pressure as based on small deflection theory, the critical buckling pressure P_cr can be obtained using the following equation:
In Eq. (1), R is the pipeline radius, E is the Young’s modulus of elasticity of the pipeline material and I is the moment of inertia of the pipeline cross-section. A similar formula has been developed by Bryan [14], i.e. Eq. (2), for a freestanding long pipeline subjected to hydrostatic pressure. The difference between Bryan’s and Bresse’s formulae is the replacement of E with E/(1-ν²). This accounts for plane strain conditions in computing the buckling pressure of infinitely long pipes.
In the above equation, D is the mean diameter of the pipeline, E is the Young’s modulus of elasticity of the pipeline material, t is the mean thickness of the pipe wall, and ν is Poisson’s ratio. The first research introducing the buckling propagation in pipelines was the work of Mesloh et al. [15] followed closely by Palmer and Martin’s study [16]. In the latter study, it was claimed that the propagation pressure can be determined using the strain energy of the collapsed cross-section of the pipe with an equation proposed for this purpose. In this research, the experimental values obtained with low diameter-to-thickness ratios (D⁄t) were greater than the predicted results. This issue is expected in deep water conditions considering the effects of plastic deformation [7]. The studies of Johns et al. & Mesloh et al. [1,15], took an experimental approach to this subject and determined the adequacy of different arrestor geometries for stopping the buckling propagation. These studies resulted in the empirical formula of propagation pressure P_pr based on diameter, thickness, and yield stress (σ_Y).
Palmer & Martin [16] proposed the following formula for predicting the buckling propagation pressure in pipelines Ppr. This equation is based on the assumption that the material is rigid and perfectly plastic. In their model, four plastic hinges govern the collapse mechanism during buckling propagation based on an energy balance.
Barlow’s formula [17], i.e. Eq. (5), is used for calculating the hoop stress in thin-walled cylinders with D0/t>20, in which D0 is the outer diameter and t is the wall thickness.
Where, Pi is the internal pressure and Pe is the external pressure applied on the pipe as shown in Figure 4, and H σ is the hoop stress in this equation. It is noted that the use of this equation is limited to thin-walled pipes [18].
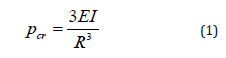
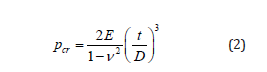
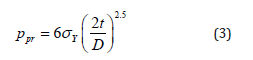
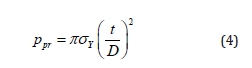
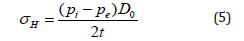
Internal and external pressures induce hoop stress, which results in expansion of the pipe’s circular cross-section. On this basis, while studying the fully- or partially-anchored pipelines, one can expect to observe the Poisson effect, i.e. the expansion or compression of material in one direction due to an external force which entails compression or expansion reaction in the other direction [19,20]. Thus, because of the Poisson effect, the hoop stress in an anchored pipeline creates longitudinal stress. Pressure-induced longitudinal stresses in an anchored pipeline can be obtained from the following equation:
Von Mises equivalent stress eq σ can be determined using Eq. (7) by considering the hoop and longitudinal stresses discussed above.

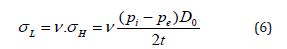
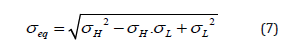
Local buckling occurs when the pipe undergoes localized deformations which involves only a small portion of the pipeline. This buckling mode occurs when the pipe wall thickness is relatively small compared to the pipe diameter. The pressure that can trigger local buckling, which is also known as buckle initiation pressure (Pi), is normally lower than the collapse pressure and has been the subject of several investigations. Shell Development Company has provided the following empirical equation for calculating the buckle initiation pressure. Eq. (8) shows that reducing the pipe wall thickness results in reduced buckle initiation pressure and increases the chance of unexpected local buckling in the weakened sections [21-23].

To read more about this article...Open access Journal of Current Trends in Civil & Structural Engineering

Please follow the URL to access more information about this article
https://irispublishers.com/ctcse/fulltext/stability-performance-assessment-of-pipelines-under-hydrostatic-pressure.ID.000524.php

To know more about our Journals....Iris Publishers

To know about Open Access Publishers