Authored by Clement Boateng Ampadu
Abstract
The T − X (W)family of distributions appeared in [1]. In this paper, inspired by the structure of the CDF in the Zubair-G class of distributions [2], we introduce a new family of distributions called the Ampadu-G class of distributions, and use it to obtain a new class of distributions which we will call the AT − X (W) class of distributions, as a further application of the T − X (W)framework. Sub-models of the Ampadu-G class of distributions and the AT − X (W) class of distributions are shown to be practically significant in modeling real-life data. The Ampadu-G class of distributions is seen to be strikingly similar in structure to the Exponentiated EP (EEP) model contained in [3], and the Zubair-G class of distributions is seen to be strikingly similar in structure to the Complementary exponentiated Weibull-Poisson (CEWP) model contained in [4].Keywords:Zubair-G; T − X (W)family of distributions; Ampadu-G
Introduction
Background on the T − X (W)family of distributions
Definition 3.1: [1] Let r (t) be the PDF of a continuous random variable T ∈[a, b] for −∞ ≤ a ≤ b ≤ ∞ and let R(t ) be its CDF. Also let the random variable X have CDF F (x) and PDF f (x) , respectively. A random variable B is said to be T − X (W)distributed if the CDF can be written as the following integral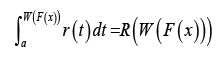
a) W (F (x))∈[a, b]
b) W (F (x))is differentiable and monotonically nondecreasing
c) limx→−∞ W(F(x))= a and limx→−∞ W(F(x))= b
Remark 3.2: By differentiating the RHS of the above equation with respect to x, the PDF
of the T − X (W)family of distributions can be obtained.
Remark 3.3: If the continuous random variable T has support [0, 1], we can take
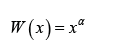
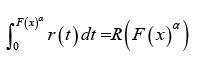
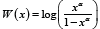 where
α > 0 . In particular, we will say arandom variable B T − X (W)
distributed of type II, if the CDF can be written as either one of the
following integrals
where
α > 0 . In particular, we will say arandom variable B T − X (W)
distributed of type II, if the CDF can be written as either one of the
following integrals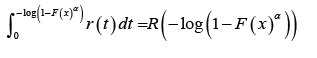
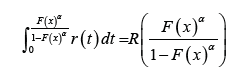
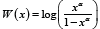 , where
α > 0 . In particular, we will say a random variable B is T − X (W)
distributed of type III, if the CDF can be written
, where
α > 0 . In particular, we will say a random variable B is T − X (W)
distributed of type III, if the CDF can be writtenas either one of the following integrals
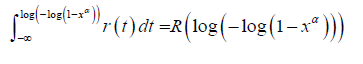
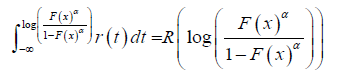
Background on Zubair-G family of distributions
Definition 3.7: [2] A random variable B* is said to be Zubair-G distributed if the CDF is given bywhere

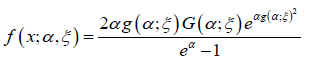
The New Family of Distributions
The Ampadu-G family of distributions
Definition 4.1: Let λ > 0,ξ > 0 be a parameter vector all of whose entries are positive, and x∈R . A random variable X will be said to follow the Ampadu-G family of distributions if the CDF is given by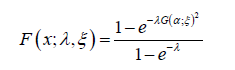
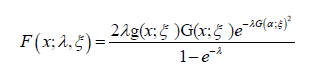
Generalized AT − X (W) Family of Distributions of type I
Definition 4.2: Assume the random variable T with support [0, 1] has CDF G(t;ξ ) andAT − X (W) distributed of type I if the CDF can be expressed as the following integral
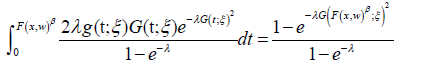
Remark 4.3: If β =1 in the above definition we say S is AT − X (W) distributed of type I
Generalized AT − X (W) Family of Distributions of type II
Definition 4.4: Assume the random variable T with support [a,∞) has CDF G(t,ξ ) andPDF g(x,ξ ). We say a random variable S is generalized AT − X (W) distributed of type II if the CDF can be expressed as either one of the following integrals
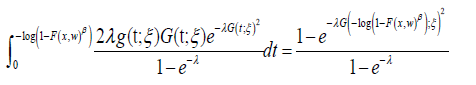
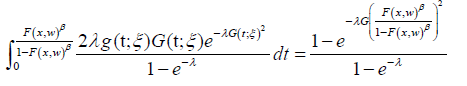 where λ,ξ ,β > 0 and the random variable X with parameter
vector ! has CDF F (x,w) and PDF f (x,w)
where λ,ξ ,β > 0 and the random variable X with parameter
vector ! has CDF F (x,w) and PDF f (x,w)Remark 4.5: If β =1 in the above definition we say S is AT − X (W) distributed of type II
Generalized AT − X (W) Family of Distributions of type III
Definition 4.6: Assume the random variable T with support (−∞,∞) has CDF G(t;ξ ) and PDF g(t;ξ ) . We say a random variable S is generalized AT − X (W) distributed of type III if the CDF can be expressed as either one of the following integrals

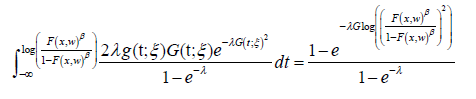
Remark 4.7. If β =1 in the above definition, we say S is AT − X (W) distributed of type III
Practical Application to Real-life Data
Illustration of Ampadu-G family of distributions
We consider the data set [5] which is on the breaking stress of carbon fibers of 50 mm in length. We assume the baseline distribution is Weibull distributed, so that for x,a,b > 0 , the CDF is given by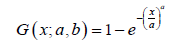
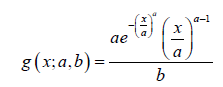
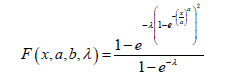
Proof. Since the baseline distribution is Weibull distributed, then for x,a,b > 0 , the CDF is given by
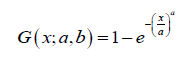
To read more about this article...Open access Journal of Annals of Biostatistics & Biometric Applications
Please follow the URL to access more information about this article
To know more about our Journals....Iris Publishers
To know about Open Access Publishers





No comments:
Post a Comment