Iris Publishers- Open access Journal of Biostatistics & Biometric Applications | Improved Algorithm of Blocking the Selected Edges in the Digraph

 

Authored by Tsitsiashvili Gurami*

Abstract

In this paper, a protein network represented by a directed graph is considered. The problem of determining the minimum number of edges that break paths from the input proteins of the network to the output ones and passing through some subset of proteins in this network is analyzing. An improved algorithm based on a selection of connectivity components in the sub-graph with dedicated subset of nodes is suggesting.

Keywords: Cluster; Digraph; Sub-graph; Protein network; Connectivity component

Introduction

In this paper, we consider a protein network represented by a directed graph (digraph) G with the set U of nodes, which are proteins and whose directed edges are paired bonds between nodes represented in the Cytoscape program. Dedicate the subset U/ ⊂U of nodes and decrease in a comparison with [1] a number of edges, which block all paths from outside of the set U/ outside of the set U/ .

Take all nodes from the subset U/ and all edges between them. These nodes and edges create directed sub-graph G/ ⊂ G. Replace all (directed) edges of the sub-graph G/ ⊂ G by undirected ones and obtain undirected graph G// . Define in the sub-graph G// all its connectivity components 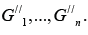 .Return directions to all edges of the sub-graph G//K and define in such a way the sub-graph k G of the digraph G, k =1,...,n.

Factorize each sub-graph Gk by a relation of cyclic equivalence and construct acyclic digraph with nodes are clusters of cyclic equivalence. In the sub-graph, Gk each cluster has out coming edges to another cluster and/or incoming edges from another cluster. If a cluster has only out coming edges to another cluster, we call it input cluster. If a cluster has only incoming edges from another cluster, we call it output cluster. In the sub-graph, Gk there is a path from input cluster to some of output clusters and there is a path to output cluster from some input ones. Any edge beginning in the sub-graph Gk does not reach another sub-graph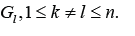 

Denote by 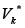the set of edges incoming to GK and by 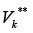the set of edges out coming from .GK It is obvious that

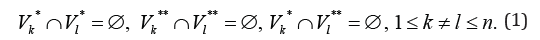
For any edge 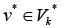there is a path to some edge 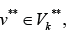and for any edge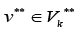there is a path from some edge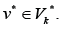Formula (1) allows to consider separately incoming and out coming edges of the sub-graphs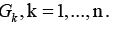 

Designate by 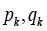numbers of edges in the sets 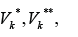.relatively. Assume that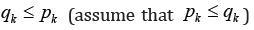and block all edges from 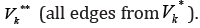In such a way, we block all paths from the outside of Gk outside of .Gk Then a number of edges blocking the sub-graph k Gk equals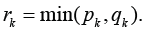Consequently to block the set U/ of dedicated nodes it is necessary only to block the following number of edges

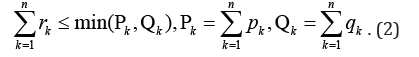
Formula (2) confirms that suggested algorithm based on the definition of connectivity components in the sub-graph G// decreases a number of blocked edges in a comparison with [1].

To read more about this article...Open access Journal of Biostatistics & Biometric Applications

Please follow the URL to access more information about this article

https://irispublishers.com/abba/fulltext/improved-algorithm-of-blocking-the-selected-edges-in-the-digraph.ID.000561.php

To know more about our Journals....Iris Publishers

To know about Open Access Publishers