Abstract
This paper provides a complete solution to the problem of minimizing the number of edges in the protein network, the removal of which blocks all paths that pass through a set of undesirable nodes. The minimization problem is reduced to the problem of minimum cut and maximum flow in a specially constructed weighted digraph with a source and a drain.
Keywords: Digraph;Ford-Fulkerson Theorem;Sub-graph; Optimal Blocking.
Problem Statement
Consider a digraphG, representing a protein network with finite sets V and E of nodes and edges respectively. In the setV there is a subset W ⊂V of undesired nodes. Contrast to the set W the subset Q ⊆W of output nodes from which edges exit to the subset U =V \W and the subset P ⊆W of input nodes to which edges enter from U.
Denoten( p) a number of edges, entering to p∈P from U, and N(q) a number of edges, exiting from q∈Q to U. Our problem is to find subsets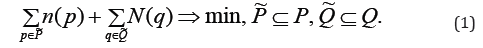 
so that their removing from the sets
breaks all paths, which transit to W from the set U , pass through W and exit back. And the number of edges to delete is minimal:
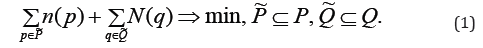
In [1] the digraphG*with the nodes set W and edges, connecting them in digraph G, is constructed. The set W of the digraph G* nodes is divided into classes of cyclical equavalence (clusters) and a relation of partial order between these clusters is defined a* ≥ b* if in the digraph G* there is a path from clustera*to clusterb*. A bipartite digraphΓ with the set of input clusters P* , the set of output clustersQ* , and the set of edges: R: (p*,q*), if p*≥q*, if p* ≥ q* This design allows for simultaneous input and output clusters, to be included into the sets P* , Q* and an edge between them is to be introduced.
The bipartite digraphΓ is divided into connectivity componenets (after deleting of edges direction) and isolated clusters are removed. In each connectivity component input or output edges are removed, depending on which number is less. But this solution is not optimal.
Search for an Optimal Solution by the Ford- Fulkerson Theorem
The Ford-Fulkerson algorithm [2] with improved additions of Edmonds-Carp [3] and Dinits [4] is used to find the maximum flow f . All algorithms for determining the maximum flow consistently find paths that increase the amount of flow. For the maximum flow found, the minimum cut is determined using well known recurrent algorithm [2].
To read more about this article..... Open access Journal of Biostatistics & Biometric ApplicationsPlease follow the URL to access more information about this articlehttps://irispublishers.com/abba/fulltext/optimal-blocking-of-undesired-nodes-in-digraph.ID.000578.php
To know more about our Journals....Iris Publishers
No comments:
Post a Comment