Authored by KC Bhuyan*
Introduction
Meta-analysis is a statistical method to combine the results of multiple scientific experiments conducted in different environments or seasons or places in order to derive a common conclusion about the suitability of the experimental materials throughout the environmental conditions. The conclusion can be drawn by estimating the parameter from the estimates of the parameter obtained from different experiments. The hypothesis regarding the parameter can be verified on the basis of the result of the individual experiment. The common conclusion can be made by combining the test results observed in different experiments. The analysis has the capacity to contrast the results derived from different experiments and to identify the patterns among experimental results in addition to have an estimate of the population parameter [1]. The technique is an important component of a systematic study of the same phenomenon investigated in different agro-climatic / environmental / socioeconomic / hygienic / political conditions.
The historical roots of met analysis can be traced back to 17th century studies of astronomy [2], while a paper published in 1904 by the statistician Karl Pearson in the British Medical Journal [3]. The first meta-analysis was identified in 1940, the book-length publication Extrasensory Perception. After sixty years, the basis of which was the experimental results of conceptually identical experiments.
[4]. The identical experiments are needed in medical science to arrive at decisions affecting clinical practice fostered the momentum toward evidence-based medicine [5-9]. These are also needed in agricultural science to select a best variety of crop or to select a best dose of fertilizer for a particular crop suitable for all agro-cli matic conditions ; in industrial sector, the industrial product is to be produced so that it is demanded by all types of customers from all walk of life in all seasons; in education sector, teaching method is to be suggested so that it will be beneficial for students of all levels of merit, etc. As an example, let us consider the study of the positive effect of a medicine which is suitable, may be in different doses, for all types of people irrespective of age, body condition score and environment. This can be done if the medicine is applied simultaneously and /or subsequently on all types of investigating units. Specifically, the prevalence of diabetes, a component of non-communicable diseases, is observed in all societies and among all types of people irrespective of age and level of obesity. In such a situation, it would be worthy, if one medicine would be discovered for all types of people irrespective of age and body mass index. For this, experiments must be conducted covering all types of people across the country or experiments are to be conducted over a period of time. This latter group of experiments are the retrospective studies which are common in medical science. These types of experiments when conducted, by necessity, may not provide similar results in all experiments. But, from the experimental results a common decision is to be drawn from all the experimental results. This leads the researchers to use the technique of meta-analysis. In near past, there were two meta-analysis [10 -11] in Indian sub-continent and in Bangladesh to estimate the rate of overweight and obesity among children and adolescents. These studies were done in analysing the dichotomous data.
One important aspect of analysis of dichotomous data is to test the association of two qualitative characters by chi-square test. When k sets of dichotomous data are available, k statistics each with (r–1) (c–1) degree of freedom (d.f) are available. When k experiments are independently conducted, the sum of the k Chisquare statistics is also distributed as Chi-square with k (r–1) (c–1) d.f. Hence a common conclusion on the independence of two characters can be made. This is one of the simplest cases of meta-analysis. This method was also proposed by Bhuyan [12]. In doing this type of analysis, a very common measure is the calculation of odds ratio and / or risk ratio. This measure is calculated to estimate the rate of risk of the incidence for a subject when he/she is exposed for the incidence. These ratios are calculated from each of k experimental results and hence a common odds ratio or a common risk ratio is the targeted analysis of the researcher. This is the most common meta-analysis in the field of medicine or biostatistics [13, 10- 11]. The common estimate of odds ratio and risk ratio are shown [ Cochran- Mantel-Haenszel estimate] using the data of k sets of dichotomous data shown below in 2 x 2 contingency table.
A 2 x 2 contingency table for i – th experiment
Here i = 1, 2, ……..., k.
The odds ratio and log of its standard error from i-th experiment are given by
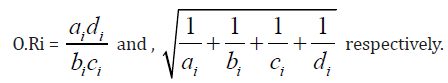
The risk ratio and log of its standard error are given, respectively by
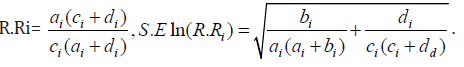
The 100 (1 – α) % confidence interval for odds ratio and risk ratio are, respectively, given by
[eln O.R. Z1 – α/2 S.R ln (O.R)],
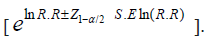
The common odds ratio and the common risk ratio are given, respectively, by
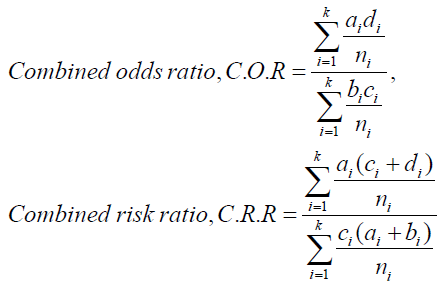
The value of C.O.R. = 1 indicates that the two characters under study are independent. Hence, it needs to test the hypothesis H0: C.O.R = 1 against alternative HA: C.O.R.≠ 1. The test statistic is
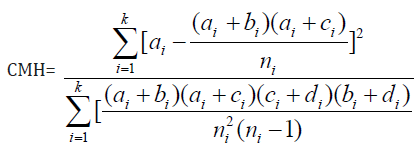
This CMH is known as Cochran- Mantel-Haenszel [13] test and it is asymptotically distributed as Chi-square distribution with 1 d.f. [15].
The analysis discussed above is suitable for discrete data. The dominant method used for continuous data are standardized mean difference estimation. Methods used in meta-analysis for post hoc analysis of findings are relatively specific to meta-analysis and include heterogeneity analysis, sensitivity analysis, and evaluation of publication bias. But all methods need the weighting of studies. Usually, studies are weighted according to the inverse of their variance. The weighted analysis does not create serious problem if fixed effect model is considered for the data. The weighted analysis for combined estimate of effect is biased. But, the bias of order 1/fi can be removed [12], where fi is the d.f. of the i-th experiment when each experiment is conducted assuming completely randomized design or randomized block design. For mixed effect model with treatment effect fixed, the combined weighted estimate of treatment effect is available. Due to the use of estimated weight, the combined estimate is biased one. However, the bias can be removed [12]. But the problem is not obviated in testing the significance of the treatment effect. The approximate analysis was proposed by many statisticians. The important works were done by Cochran, Cochran and Carroll and others [16 -19]. Later on, Bhuyan [12] suggested a method to select a stable group of treatments suitable for all environmental / experimental conditions. The results of the stable group of treatments are to be analysed to have a combined estimate of treatment effect. The test of the significance of treatment effect can be performed for each experiment separately. For common conclusion the p-values of each experiment can be combined according to the suggestion of Fisher [20]. The combined estimate of treatment effect and the common satisfactory decision regarding the significance of treatment effect were also suggested [12].
Some Result of Meta-Analysis
As an example of meta-analysis for odds ratio and risk ratio, let us discuss the results of two experiments presented in Table 1 [21] and Table 2 [22]. Both the data set are related to the study of association of prevalence of non-communicable diseases (NCDs) with residential origin of some adults in Bangladesh investigated in two different occasions by different groups of investigators (Table 1&2).
As a first step of analysis, let us consider the combined odds ratio and combined risk using the data of Table 1 and Table 2. From the first table the value of odds ratio was observed (O.R.)1=2.37 with variance Vln (O.R.)1 = 0.08196. The risk ratio was (R. R)1= 1.23 with variance Vln (R.R)1= 0.00186.The results indicated that rural adults were more than two times exposed to NCDs compared to urban adults. From the second table these results were (O.R )2=1.60 with variance.
Vln (O.R)2=0.02201; (R.R)2= 1.24 with variance Vln (R.R)2= 0.006952. It was noted from second study that the rural adults were 60.0 per cent more exposed to NCDs compared to urban adults and their risk for prevalence of NCDs was 24 % more compared to the risk of urban adults. The confidence interval for these odds ratio and risk ratio were [ 0.60,2.93]; [1.15,1.31] and [ 1.32,1.88]; [1.08,1.40].
The objective of both the studies was same but analytical results did not provide the same idea about the prevalence of NCDs among rural people compared to urban people. The problem would be obviated if it would be possible to have a common estimate of odds ratio for a common conclusion using both the data set. The common estimate of odds ratio and risk ratio were given here.
The common estimate of odds ratio and common estimate of risk ratio from both the data set were calculated. These results were O.R = 1.25 and R.R = 1.23. The results indicate that rural adults were 25% more exposed to prevalence of NCDs compared to urban adults and their relative risk is 23% more.
To read more about this article......Open access Journal of Archives in Biomedical Engineering & Biotechnology
Please follow the URL to access more information about this article
To know more about our Journals...Iris Publishers





No comments:
Post a Comment