Iris Publishers- Open access Journal of Engineering Sciences | Prediction of Deflection Progression of RC Beams Strengthened with NSM FRP Composites

 

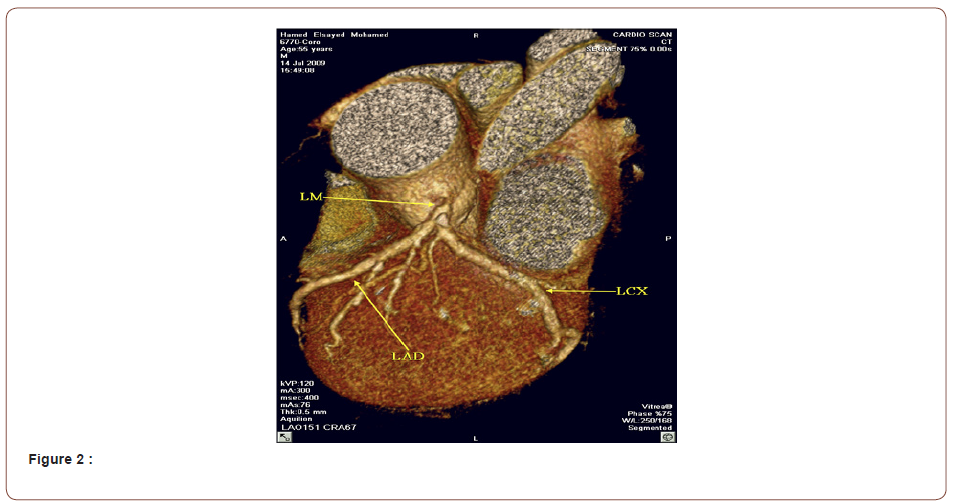
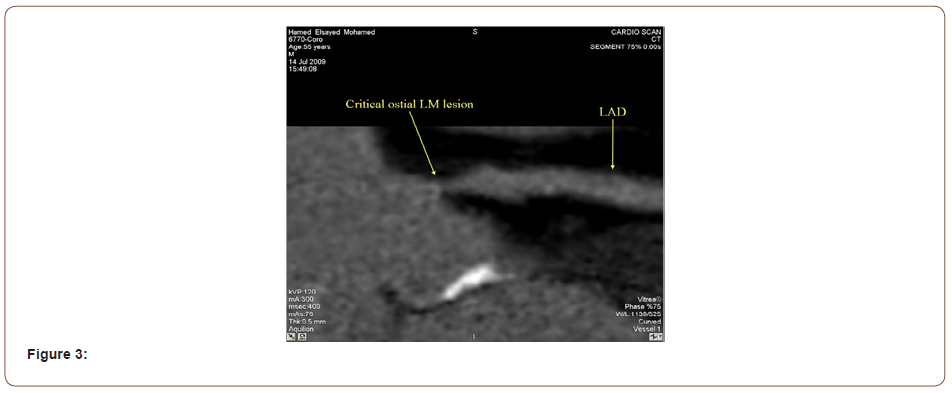
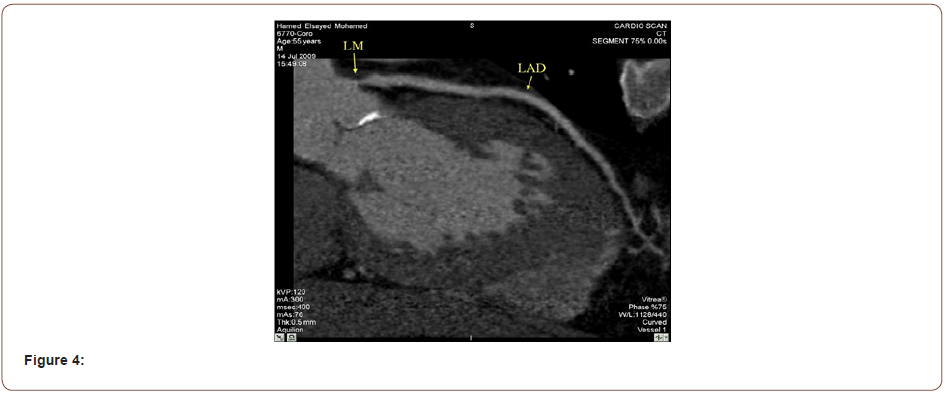
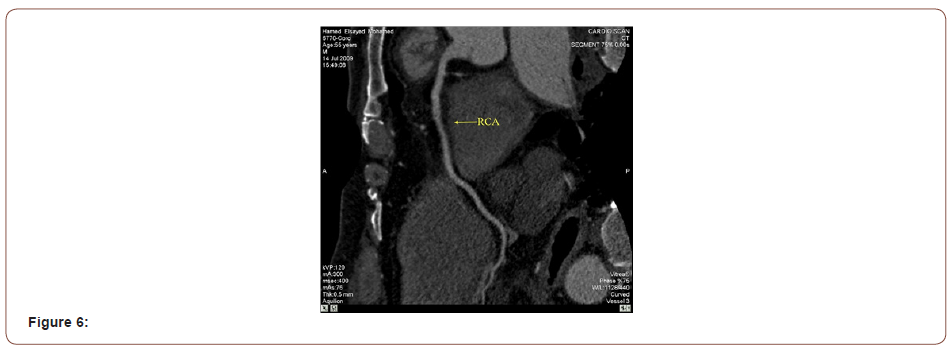
Authored by Tamer Eljufout*,

Abstract

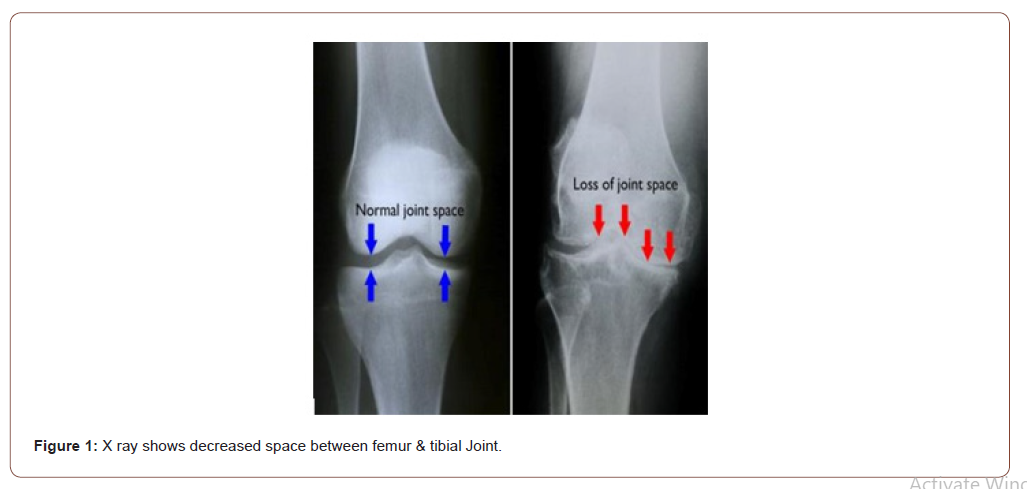
The deflection progression of Reinforced Concrete (RC) beams under cyclic loads gives a reliable indication of the accumulation of fatigue damages. Excessive increase in deflection raises a red flag for an immediate need for rehabilitation. This paper presents an analytical model for predicting the deflection evolution of RC beams strengthened with Near Surface Mounted (NSM) Fiber Reinforced Polymer (FRP) reinforcement. The model was validated based on experimental and numerical analyses. A three-dimensional strengthened RC beam was modeled using ANSYS software with similar dimensions and material properties of specimens that were experimentally tested. Numerical simulations were performed for the RC beam under constant amplitude cyclic loads. The analytical model predicted the increase in deflection due to the cyclic creep of concrete during the fatigue life of RC beams. A satisfactory correlation and consistency were noticed between the numerical and analytical predictions with a mean error of deflection less than 9.5%..

Keywords: Bridges; RC beams; Fatigue; Finite element analysis; NSM

Introduction

Many RC bridges all over the world are approaching the end of their design life. Therefore, bridges safety has been in the spotlight to prevent any serious structural problems that might lead to loss of life [1,2]. Efficient and practical strengthening techniques are needed to prevent potential disasters. FRP composite materials have proven their effectiveness in the strengthening of existing structures [3-6]. The development of deflection of RC beams gives a reliable indication of the damage accumulation along with the service life. Different factors affect the deflection progression of a RC beam, such as concrete creep, shrinkage, fatigue, overloading, and environmental exposures. Fatigue is the most critical factor that might cause a sudden failure to structural members. External bonded (EB) and NSM are the most common practical application techniques of FRP materials. These techniques are becoming extensively used in the strengthening field of RC bridges [7]. The fatigue behavior of the NSM CFRP strengthening technique is still not fully investigated. Moreover, the current design codes and guidelines do not provide practical design guidelines for structural engineers to predict the fatigue behavior of RC beams strengthened with NSM FRP [8]. This study investigates the ability of the analytical model proposed by Balaguru & Shah [9] for predicting the deflection response of RC beams strengthened with NSM FRP reinforcement under cyclic loading.

The Analytical Model

Balaguru and Shah [9] proposed an analytical model for predicting the accumulation of deflection of non-strengthened RC beams subjected to cyclic loading. The model ignores different factors, such as the shrinkage effect, concrete mix proportion, and the age at loading. The deflection of a RC beam is calculated on the basis of the effective moment of inertia taking into consideration the reduction in stiffness due to the creep strain after several load cycles. Based on their model, the increase of deflection is attributed to the concrete creep in the compression zone, reduction in stiffness due to the flexural cracks, and the strain-softening of steel reinforcement.

The cyclic creep strain of concrete can be expressed as determined by Whaley and Neville [10]:

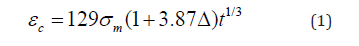
The previous equation is used to develop a cycle-dependent secant modulus for concrete in compression as follows:

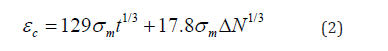
A cycle-dependent secant modulus of concrete under compression is presented by:

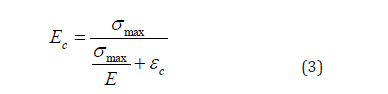
The reduction in stiffness of RC beam due to the fatigue tensile cracking and debonding must be considered. The effective moment of inertia expressed as:

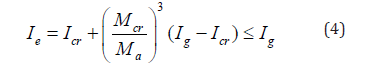
The cracking moment is giving by:

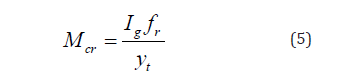
The stiffness of the strengthened RC beam is reducing with the increase of the number of cycles. The relation between the initial modulus of rupture and its value at a given number of cycles is:

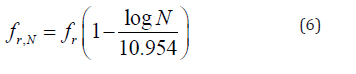
The deflections of short-term static loading are calculated as follows:

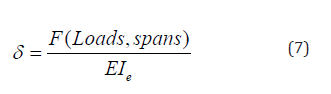
Where 𝐹 (Loads, spans) is a function of the load and span arrangement, and 𝐸𝐼𝑒 is the initial effective stiffness of the RC beam.

The deflection after a given number of cycles is presented as:

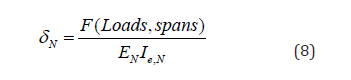
Where 𝐼𝑒,𝑁 is given by:

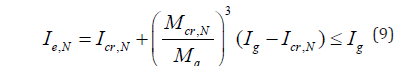
The cracking moment at a given number of cycles is:

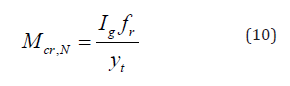
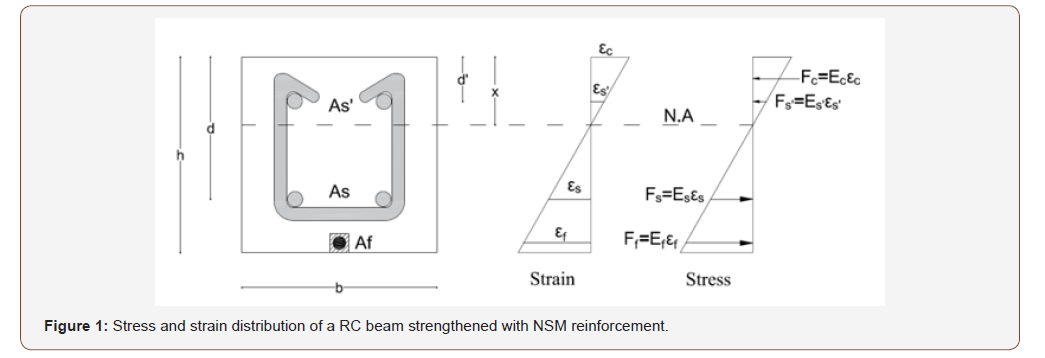
The classical beam theory can be used to determine the stress distribution along the RC beam section, as shown in Figure 1. The contribution of FRP reinforcement is considered similar to the contribution of steel reinforcement. The depth of the neutral axis (x) was found using the force equilibrium along the beam’s section, as follows:

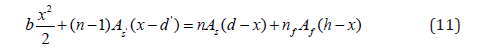
The modular ratio of steel reinforcement is given by:

The modular ratio of FRP reinforcement is given by:

The gross moment of inertia is given by:

The moment of inertia of the cracked section is calculated by:

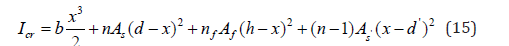
The Numerical Model

A strengthened RC beam was modeled with similar dimensions and material properties of specimens that were experimentally tested by Eljufout and Toutanji [11]. A three-dimensional finite element RC beam was modeled using ANSYS (2015). The static and fatigue tools in ANSYS were utilized in this study. The fatigue tool allows the determination of fatigue damage and life using a stress- life or strain-life approach. Static analyses were performed to calibrate the simulated RC beam. The fatigue analysis was performed in increments to obtain the model’s responses along with the fatigue life. The obtained data includes the deflection and strain progression with respect to the number of cycles.

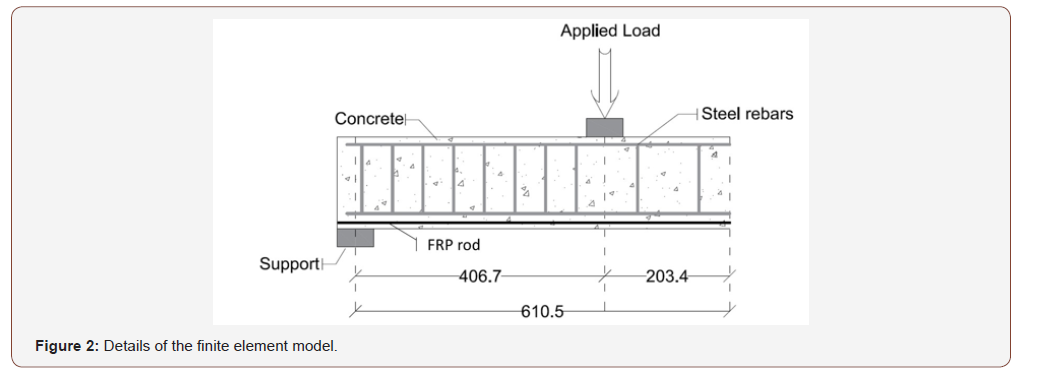
The model has a total length of 1221mm and a square crosssection with a width and depth of 152.4mm. The steel reinforcement consists of four 12mm diameter rebars, two rebars in the tension zone and another two rebars in the compression zone. The RC beam is strengthened with a 9.6 mm diameter CFRP rod placed in the beam’s soffit, Figure 1. The fatigue properties of the modeled RC beam were defined based on the empirical S-N curves that were developed in the study done by Eljufout and Toutanji [11] for RC beams strengthened with NSM CFRP. The model is a simply supported beam according to the configuration of experimental tests. An end of the beam was modeled as a hinge support that is constrained in both horizontal and vertical direction. Whereas the other end was modeled as a roller support that is constrained only in the vertical direction. A steel plate was modeled to simulate a two-point bending spreader beam. This allows the applied load to transfer in a constant form of pressure. Steel plates and supports were assumed to have a perfect bonding with the concrete.

Due to the symmetry of the RC beam and the testing configuration, only half of the RC beam was modeled with the proper boundary conditions to reduce the computational time and the needed storage of data. The RC beam’s symmetry was simulated by restraining the displacement in the plane perpendicular to the plane of symmetry. A convergence study was performed to determine the appropriate element size. The Newton-Raphson approach was utilized for the nonlinearity of the model during the static analysis (Figure 2).

The concrete and epoxy used in this study were considered as quasi-brittle materials with different responses under compression and tension loads. The SOLID65 element was employed to model concrete and epoxy resin. This element has eight nodes with three degrees of freedom at each node, translations in the nodal x, y, and z directions. Moreover, the element is capable of predicting the nonlinear behavior using a smeared crack approach, which allows the model to simulate the concrete and epoxy resin failure modes accounting for both cracking in tension, crushing in compression, plastic deformation, and creep in three orthogonal directions [12]. The element requires linear and multilinear isotropic material properties. Thus, the ultimate compressive and tension uniaxial strengths are needed to define the failure criterion of concrete and epoxy resin. Von-misses’ criteria were considered based on the study performed by William and Warnke [13]. The SOLID65 element starts cracking once any of the principal tensile stresses in any direction exceed the maximum defined tensile principal stress of the defined material. Likewise, the element starts crushing once the principal compressive stresses exceed the defined maximum compressive stress. The condition of the crack face was presented by the shear transfer coefficients for an open and closed crack, and was 0.3 and 0.8, respectively. Typical shear transfer coefficients range from 0.0 to 1.0, where 0.0 represents a smooth crack (complete loss of shear transfer) and 1.0 representing a rough crack (no loss of shear transfer).

Different analytical models have been proposed to predict the stress-strain response of a brittle material. The analytical model that was proposed by Ali et al. [14] was used in this study. Concrete has a perfect linear elastic behavior within the first third of its ultimate compressive strength. After reaching the ultimate strength, concrete starts to soften and crushing. The complete failure occurs once the concrete reaches the ultimate strain. The SOLID65 element was defined accordingly to avoid convergence problems. The required stress-strain curve was developed based on the ultimate compressive strength obtained by experimental tests and using the following equation:

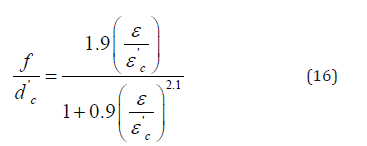
The modulus of elasticity and tensile strength were calculated by the following equations [15]:

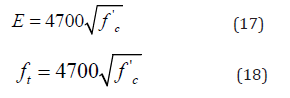
All the defined properties in equations (17) and (18) are in mega-pascal (MPa). The flexural and shear reinforcements were included in the RC beam model. The steel and CFRP reinforcements were modeled by a LINK180 element. This element is a three degrees of freedom spar element with two nodes, and it has the ability for translations in the nodal x, y, and z directions. The element is capable of plastic deformation and it was modeled as an elastic-linear hardening material BKHM (Bilinear Kinematic Hardening Model), and identical in tension and compression. A perfect bonding was assumed between concrete, steel rebars, and CFRP reinforcement.

Table 1: Material properties of concrete and steel reinforcement.

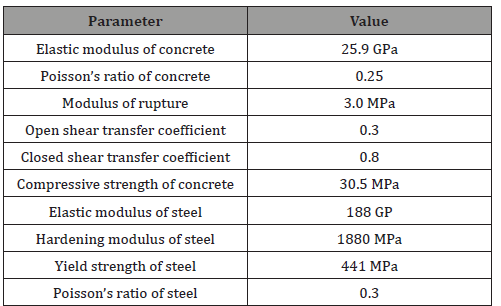
The SOLID45 element was used for modeling the rigid steel support and loading plate. This element has eight nodes with three degrees of freedom at each node, translations in the nodal x, y, and z directions. This element was assumed to be a linear elastic material with an elastic modulus of 188 GPa and Poisson’s ratio of 0.3. The steel support and loading plate were modeled to obtain a constant stress distribution along the element’s cross-section. This helps to maintain a better convergence by avoiding concrete crushing. Both the steel support and loading plate have the same dimensions of 152.4 mm × 60 mm × 30 mm. Tables 1 & 2 present the material properties of the RC beam.

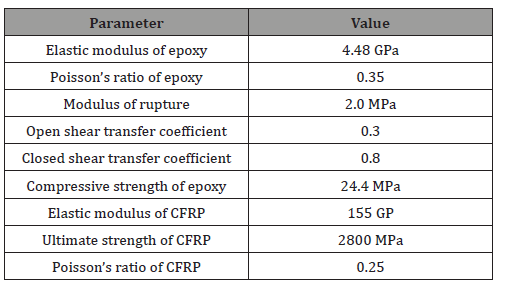
Table 2: Material properties of epoxy and CFRP reinforcement.

Discussion

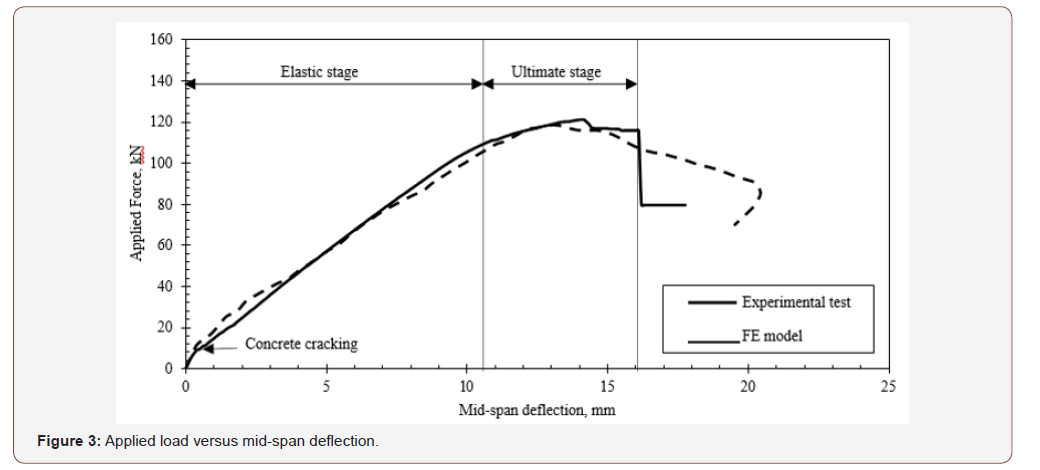
The model was validated under monotonic and fatigue loading with respect to the experimental results that were obtained in a study done by Eljufout and Toutanji (10). The model responses correlate satisfactorily with the experimental data at all stages of the monotonic and cyclic loading [16,17]. A comparison between the obtained numerical and experimental static behaviors is presented in Figure 3. Two significant stages can be characterized in the static behavior of the RC beam; linear elastic stage and nonlinear ultimate stage. The experimental yield load was determined as 105.3 kN at a deflection of 10.0mm. The numerical yield load was 106.2 kN at a deflection of 10.6mm.

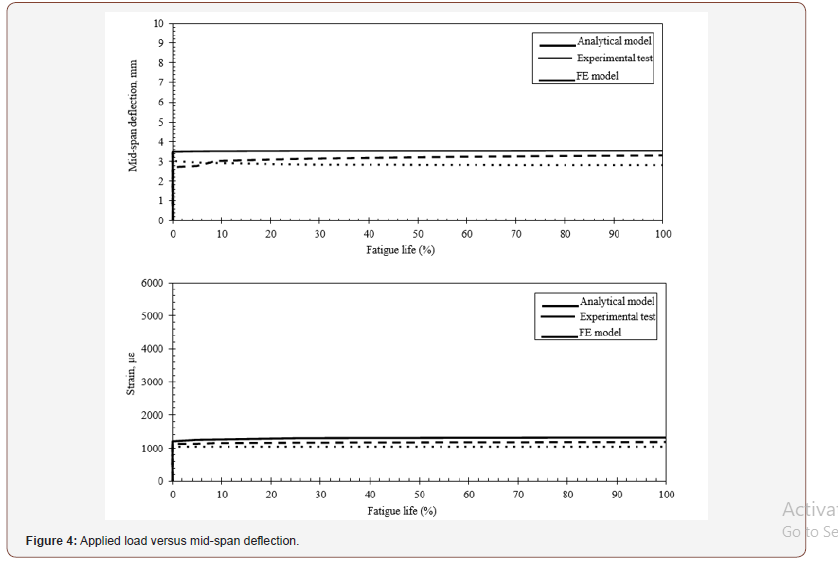
The model was subjected to a constant cyclic load ranges of 31 kN and 46 kN, Figures 4 & 5. A good precision was noticed between the FE simulations and experimental tests. The maximum deviation between the numerical and experimental results for deflection under cyclic loading is less than 17%.

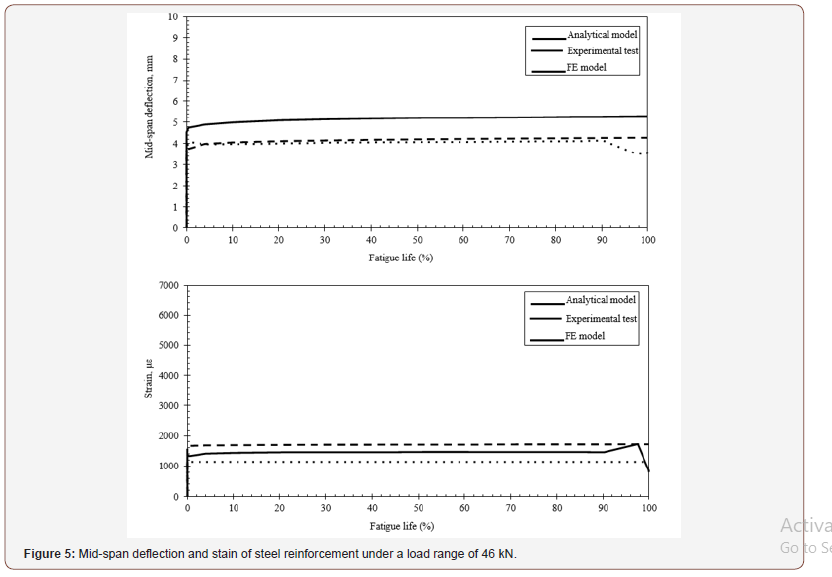
Numerical and analytical analyses were carried out for four strengthened RC beams. Specimens “B01”, “B02”, “B03”, and “B04” were subjected to 31, 36, 41, and 46 kN cyclic load ranges, respectively. The obtained strain of tension steel reinforcement was less than that observed during the experimental tests. The deflection of the analyzed RC beams was accumulating with the applied load cycles. All specimens experienced an initial rapid increase of the mid-span deflection, then followed by a steady rate of deflection accumulations. The deflection exhibited a dramatic increase just before failure in both the experimental and numerical simulations [18,19].

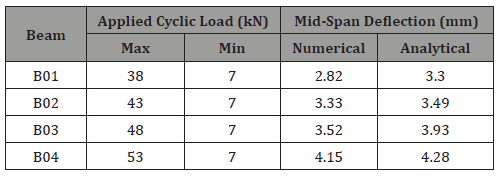
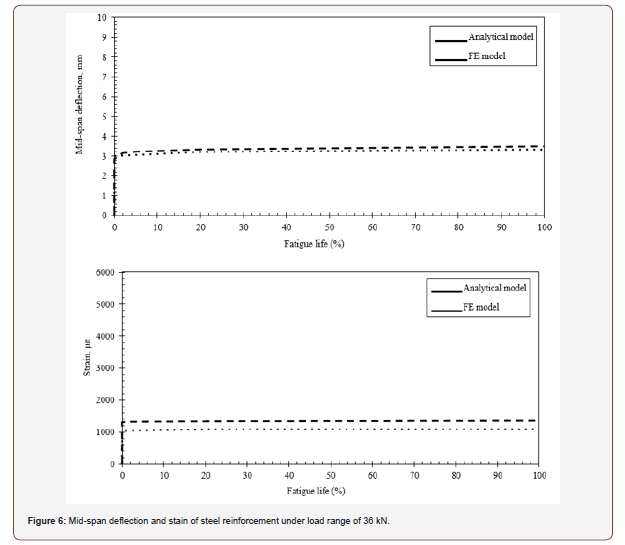
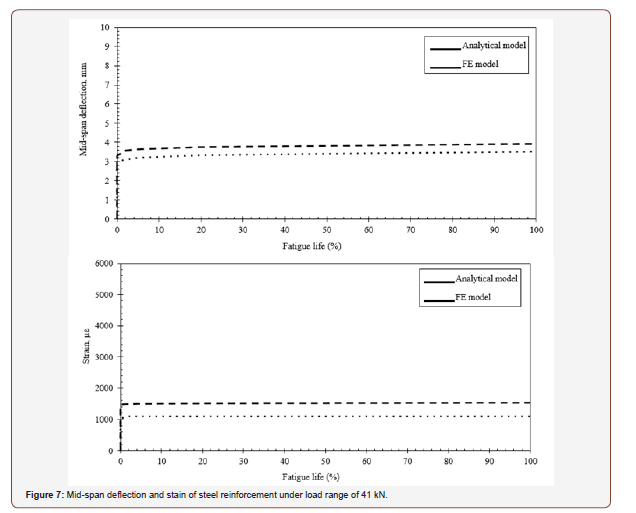
Table 3 summarizes the obtained results of the deflection progression of numerical and analytical analyses. The mean numerical to analytical deflection ratio is 0.92 with a standard deviation of 0.3 mm. Comparison of the obtained mid-span deflection and strain of tension steel reinforcement is presented in Figures 6 & 7 for specimens “B02” and “B03”. The analytical model predicted the increase in strain due to the cyclic creep of concrete along with the fatigue life of RC beams. A good correlation was noticed of specimens “B01” and “B04”. The analytical and numerical predictions of deflection development for specimens “B02” and “B03” was consistency along with the fatigue life. The analytical predictions of deflection increase gradually with the increase of applied cycles. The predicted values of deflection are close to the numerical results at all stages of the fatigue life and under different loading conditions. The mean error of deflection is less than 9.5%. The error is calculated by dividing the absolute difference between the predicted and measured values of deflection over the measured value.

Table 3: Comparison of the obtained deflection progression.

Conclusion

An analytical model was employed to predict the development of deflection of RC beams strengthened with FRP reinforcement under cyclic loading. With reference to the numerical and analytical analyses that were performed, the following conclusions can be drawn:

• The analytical model proposed by Balaguru & Shah (6) gives practical predictions of the deflection development of RC beams strengthened with NSM reinforcement. The obtained results are in good agreement with the experimental and numerical results.

• RC beams strengthened with NSM CFRP reinforcement degrade gradually with the increase of the number of cycles based on the predictions that are given by the numerical and analytical analyses.

To read more about this article...Open access Journal of of Engineering Sciences

Please follow the URL to access more information about this article

https://irispublishers.com/gjes/fulltext/prediction-of-deflection-progression-of-rc-beams-strengthened-with-nsm-frp-composites.ID.000561.php

To know more about our Journals...Iris Publishers

To know about Open Access Publishers

Iris Publishers-Open access Journal of Orthopedics Research | Obesity Invites Osteo-Arthritis in Young Women Weight Reduction be the Main Stay of Management! A Case Study

 

Authored by Pallavi*,

Abstract

Knee osteoarthritis (OA), also known as degenerative joint disease of the knee, is typically the result of wear and tear and progressive loss of articular cartilage. Age, weight and gender are the predisposing risk factors and symptoms are swelling, pain and stiffness at knee joint. We here present a case of 43-year-old housewife reported with pain, swelling and stiffness at right knee on 5 May 2021 was taken to nearby orthopedician. After physical examination and radiological investigation, she was diagnosed with knee osteoarthritis. He treated her with some analgesics and anti-inflammatory drugs and suggested to take physical therapy and counselled for weight reduction. In a follow up visit she had reduced her weight by 3 kgs in a month’s time and was doing fine. We infer that weight of an individual plays an important role in the incidence of knee osteoarthritis.

Background

Knee osteoarthritis (OA) is the most common joint disease. Almost everyone will eventually develop some degree of osteoarthritis. The most common cause of osteoarthritis of the knee is age. Some factors increase the risk of developing significant arthritis at an earlier age. Weight is one such variable that increases pressure on all the joints, especially the knees. a 5-unit increase in body mass index was associated with a 35 per cent increased risk of knee OA [1]. Women ages 55 and older are more likely than men to develop osteoarthritis of the knee. We report a case in a relatively young women of 43 years but obese lady and with no familial history, in contradiction to known factors and managed by standard practices of weight reduction, physiotherapy and NSAIDs in the initial few days for pain relief.

Introduction

Knee osteoarthritis (OA) is the most common joint disease, in which the articular cartilage present between the femur and tibial bone joint will damaged. It is the second most common rheumatologic problem and the most frequent joint disease with a prevalence of 22% to 39% in India [2] OA is more common in persons aged 55 years and above, Obesity and gender i.e., more among women than men, are higher risk factors and the prevalence increases dramatically with age Osteoarthritis is a progressive disease that may eventually lead to disability. Common clinical symptoms include, a) Knee pain that is gradual in onset and worse with activity, b) Knee stiffness and swelling, c) Pain after prolonged sitting or resting. However, symptoms become severe, more frequent over time. The rate of progression also varies for everyone.

Case Presentation

On 5th May 2021, a short obese lady of 43 years, consulted a private Orthopaedic specialist with complaints sweeling, pain and stiffness in the Right knee joint and restricted movements. The pain and stiffness were first noticed three months ago. The pain used to aggravate after long walks, staring up and down, sitting on ground for long time and easing factor was rest. At night and morning, the pain was severe. Day by day her pain was increased and forced her to seek care.

Orthopedician Findings

Physical examination like palpation for tenderness and warmth was positive. There was swelling, touch elicited tenderness, warmth and restricted movements

Weight:75kgs

Height: 151cm

Built: short and obese.

BMI= 32.9kg/m2- Obese class 1

Investigations: x-ray; right knee -AP and lateral view (Figure 1)

Diagnosis: Based on history, physical examination findings and x ray diagnosed as having Rt. Knee osteoarthritis.

Treatment: For immediate relief she was put on following drugs.

Pharmacological Therapy

1.Tab Spade Ap- pain relieving medicine (containing Aceclofenac 100mg, Paracetamol 325mg and serrati peptidase 15mg) daily two times morning and night after food for 5 days.

2.Tab Calcium 1.5g- daily two times morning and evening after food for 10 days

3.Tab Trueceprol- Oxaceprol anti-inflammatory drug (containing Oxaceprol 600mg) daily two times morning and night after food for 5 days.

4.Tab Razo d- proton-pump inhibitors. It works by decreasing the amount of acid made in the stomach (containing Pantoprazole 40mg) for 5 days

5.Inj dynapar-pain killer (containing diclofenac 75mg/ml) given at hospital

Orthopaedician advised her for losing weight and regular exercise and counselled to avoid activities that put load on her knee joint such as squatting, ascending, and descending of stairs, jumping, running.

Physical therapy

A schedule of physiotherapy was recommended and initially done under the guidance of physiotherapist with the goal of increasing the range of movements and flexibility that could ease her pain. Muscle strengthening exercise such as Quad sets, Hamstring sets, Straight leg raises, Bridging, Knee extension, Heel raises, Butt kicks was suggested IFT (INTERFERENTIAL THERAPY) was given by physiotherapist to relieve pain, and to reduce swelling for 5 days.

Bracing

Knee unloader was prescribed to relieve pain and for knee support.

Follow up tip

• 1st follow-up: Followed up after 5 days, of therapy, the pain and sweeling had subsided after 2 days and was almost negligible on the day od visit after completing IFT therapy and medicine course. She was doing well after stopping IFT and medications there was no pain and sweeling. Was advised to continue with her knee strengthening exercise and wearing knee brace while working and standing for long hours.

• After One Month: Followed after one month she was doing fine now and had reduced 3 kgs of weight and continued with her weight loss efforts.

Discussion

Osteoarthritis (OA) a common disease of aged population and one of the leading causes of disability. Incidence of knee OA is rising by increasing average age of general population. Age, weight, trauma to joint due to repetition of movements in particular squatting and kneeling are common risk factors of knee OA [3]. In our case though age was not in favour but her weight was the main reason for the condition as Obesity can predispose patients to suffer from knee OA [4].

A typical management starts with topical and oral NSAIDs to reduce the pain, tenderness, rigidity and improve movements, as was done our case. This should be quickly followed as soon as the acute pain is reduced with non-pharmacological therapies the longterm solution of treatment for knee OA. Our case was also advised on the same line for Weight management that played an important role in symptom relief and help weight. body weight influences the severity of OA; obese individuals have significantly more severe joint degeneration in the knees compared with normal weight or underweight individuals [1,4].

Obesity is the greatest modifiable risk factor for OA. Coggon et al reported that subjects with a BMI>30 kg/m2 were 6.8 times more likely to develop knee OA than normal-weight controls [1]. Case reported was class 1 Obese and weight reduction was badly needed. Fortunately, the client followed the regimen advised and saw the result within one month. Recent meta study analysis reported that risk of OA increases by 35% with every 5 kg/m2 increases of BMI [5]. case-control study was conducted in Utah. Between 1992 and 2000, 840 hip and 911 knee joint replacement surgery patients. Concluded that there is association between obesity and osteoarthritis [6].

Knee replacement may be indicated in the following cases

Severe knee pain or stiffness that limits everyday activities, Moderate or severe knee pain while resting, Chronic knee inflammation and swelling that does not improve with rest or medications, Knee deformity, Failure to substantially improve with other treatments [7].

Treatment suggested in this case was in line with the standard operation procedures for knee osteoarthritis 2017 of the ministry of health and family welfare, GOI.

Conclusion

Many studies show that obesity is one of the main risk factors for knee osteoarthritis. So, it is very important for any person who is obese even before diagnosed with knee osteoarthritis to loss weight and maintain it. Knee strengthening exercises also plays an important role to reduce the load on knee.

Learning outcomes/Take home message

• Knee osteoarthritis is common among Obese women

• Importance of physiotherapy and IFT therapy in reducing pain and swelling.

• Knee strengthening exercises and weight loss plays vital role.

• Maintaining body weight and regular physical exercises are important for every individual.

To read more about this article...Open access Journal of Orthopedics Research

Please follow the URL to access more information about this article

https://irispublishers.com/gjor/fulltext/obesity-invites-osteo-arthritis-in-young-women-weight-reduction-be-the-main-stay-of-management.ID.000565.php

To know more about our Journals...Iris Publishers

To know about Open Access Publishers

Iris Publishers-Open access Journal of Biomedical Engineering & Biotechnology | Role of CT Angiography in Detection Left Main disease in Asymptomatic Patients

 

Authored by Mosaab Akram Elshaer*,

Abstract

Background
For decades, many investigators have been trying to find the “factors” that increase the risk of coronary artery disease , A lot of cases reported for Asymptomatic patients or very mild symptoms and tendence to be coronary artery disease and in many cases, it could be critical situation.
Despite these massive efforts and findings, still some young individuals suffer from myocardial infarction without any “traditional” risk factors.
Coronary calcium score has emerged as a reliable tool to add to the already known mix of the risk factors to assess someone’s future risk of acute coronary syndromes by identifying atherosclerosis. Atherosclerosis, an inflammatory process in the arterial wall, starts at young ages and results in the formation of “plaques” in the arterial wall. As we age, the process of calcification begins in these plaques. We can identify the calcium in x-ray images, which confirms the underlying plaque in the arterial wall. These “plaques” are the main precursors of myocardial infarction. The CT can play important role in detection the coronary artery disease and evaluate the severity of the stenosis and its location.

Case Presentation

• Male patient, 50 years old, Mediterranean background, not diabetic, not hypertensive, nor hyperlipidemic, no significant medical history and takes no medications. He does not use tobacco, alcohol, or illicit drugs. No family history of medical disease.
• The patient has very mild occasional chest discomfort that’s not related to activities and has no precipitating factors. No dyspnea, no orthopnea.
• On physical examination: Temperature is 37c (99.5F) Blood pressure 120/80 mm, pulse is 90/m and respiration are 16/min. On Auscultation no heart sounds, no murmurs, The Lungs are clear. There is no peripheral edema.
• Electrocardiogram shows no significant changes. Echo shows Ejection fraction 56%, No resting wall motion abnormalities.

C.T Coronary angiography Findings

Left main coronary artery (L.M): is an average caliber atherosclerotic vessel showing an ostial non calcified plaque causing critical lumen narrowing; the LM is seen originating normally from the left coronary cusp, it ends by bifurcating into LAD and LCX. Left anterior descending coronary artery (LAD): is an average caliber atherosclerotic long vessel showing several noncalcified plaques throughout its course with no significant stenoses. It gives origin to three average caliber normal diagonals; the LAD ends by wrapping around the apex. Left circumflex coronary artery (LCX): is an average caliber non-dominant atherosclerotic vessel, giving origin to an average caliber long OM branch then the LCX continues as a small caliber vessel, the LCX and its OM branch are free of significant lesions. Right coronary artery (RCA): is a dominant average caliber atherosclerotic vessel, it gives origin to a small conal and RV branches and ends by bifurcating into average caliber PDA and PLB; the RCA and its branches show several nonocclusive plaques. Coronary Impression: Atherosclerotic CAD. Critical ostial LM stenosis with no other significant lesions.

C.T coronary calcium score report

(Table 1) This is the total amalgamation of a calcium score of 37 in the left main coronary artery, 8 in the right coronary artery, 0 in the left anterior descending coronary artery, 0 in the circumflex artery and 0 in the posterior descending artery.

Table 1: Calcium Plaque Burden.

Calcium Percentile Score

Total calcium score of 53 is between the 50th and 75th percentile for men between the ages of 55 and 59

This means that 50 percent of people this age and gender had less calcium than was detected in this study. The following graph shows the distribution of total calcium scores for each age group by percentiles. Your calcium score, relative to other age groups, is indicated by the highlighted square in the graph (Figure 1). [1] Callister TQ et. al., Coronary Artery Calcium Scores on Electron Beam Computed Tomography: JACC 1999. 33 (Supl.): 415A [1,2].

Translation Of Calcium Score

(Table 2) [2] Mayo Clinic Proceedings, March 1999, Vol. 74. Findings based on EBCT data. [3] Carr JJ, et. al., Evaluation of Subsecond Gated Helical CT for Quantification of Coronary Artery Calcium and Comparison with Electron Beam CT.; AJR 2000; 174: 915- 921

Table 2:

CT Cardiac Functional Analysis Report

Table 3:

(Table 3) Normal left ventricular systolic function with no resting SWMA. There are no calcifications within mitral and aortic annuli, including valves. There is no pericardial or pleural effusion. There is no aneurysm or dissection of the thoracic aorta [3,4]. Impression: Atherosclerotic CAD. Critical ostial LM stenosis with no other significant lesions.

• Calcium Score is calculated to be 53 by Agatston Score. Normal LV EF (56%) with no resting SWMA’s (Figures 2-8).

Conclusion

C.T angiography is having a good diagnostic value in detection of the left Main coronary artery disease.

To read more about this article....Open access Journal of Biomedical Engineering & Biotechnology

Please follow the URL to access more information about this article

https://irispublishers.com/abeb/fulltext/role-of-ct-angiography-in-detection-left-main-disease-in-asymptomatic-patients.ID.000640.php

To know more about our Journals...Iris Publishers

To know about Open Access Publishers