Authored by Nguyen Van Hung*,
Abstract
This work studies temperature-dependence of Debye-Waller factors of semiconductors presented in terms of cumulant expansion in extended X-ray absorption fine structure (EXAFS). The advances in these studies are succeeded based on further development of the anharmonic correlated Einstein model derived primary for fcc crystals into the one for applying to semiconductors and for creating a method having the advantage that all considered quantities are provided based on only the calculation or measurement of second cumulants. Analytical expressions of three first EXAFS cumulants have been derived. They describe the thermodynamic and anharmonic properties and contribute to accurate structural determination of semiconductors. The theory simplifies the many-body task into the one of one-dimensional model with taking the many-body effects into account based on the first shell near neighbor contributions to the vibration between absorber and backscattered atoms. Morse potential is assumed to describe single-pair atomic interaction. The results calculated using the present theory and those obtained by the created method for Ge having diamond structure are found to be in good agreement with experiment and with those of other theorie.
Keywords: Temperature dependence; Debye-Waller factor; Cumulant expansion; Anharmonic correlated einstein model; Semiconductor
Introduction
Extended X-ray Absorption Fine Structure (EXAFS) has developed into a powerful technique for providing information on the local atomic structure and thermal effects of substances. The formalism for including anharmonic effects in EXAFS is often based on the cumulant expansion approach [1] from which the expression for anharmonic EXAFS is given by
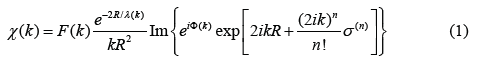
where F(k) is the real atomic backscattering amplitude, k and λ are the wave number and mean free path of the photoelectron, respectively, ɸ is net phase shift and σ(n) (n = 1, 2, 3, …) are the cumulants describing Debye-Waller factor (DWF).
In this expression of EXAFS the even cumulants contribute to the amplitude, the odd ones to the phase of EXAFS spectra, and they also account for the net thermal expansion (first cumulant), the mean square relative displacement (MSRD) (second cumulant) and the asymmetry of the pair distribution function (third cumulant). Consequently, the lack of the precise DWFs has been one of the biggest limitations not only to accurate structural determinations but also to specifications of the thermodynamic and anharmonic properties of materials from EXAFS data. Therefore, investigation of DWFs is of great interest.
The purpose of this work is to study temperature-dependence of DWFs of semiconductors presented in terms of cumulant expansion in EXAFS. The most advantageous developments in these studies are presented in Section 2. They are succeeded based on the further development of the anharmonic correlated Einstein model (ACEM) [2] derived primary for fcc crystals, into the one for applying to semiconductors and for creating a method having the advantage that all considered quantities are provided based on only the calculation or measurement of second cumulants. Analytical expressions of three first EXAFS cumulants have been derived. They describe the thermodynamic and anharmonic properties and contribute to accurate structural determination of semiconductors. The theory simplifies the many-body task into the one of one-dimensional model with taking the many body effects into account based on the first shell near neighbor contributions to the vibration between absorber and backscattered atoms. Morse potential contained in the derived anharmonic effective potential is assumed to describe the single-pair atomic interaction. In Section 3 the results calculated
using the present theory and those obtained by using the created method, i.e., from the available theoretical [3,4,10] or experimental [5-7] second cumulants of Ge having diamond structure are compared to experiment [5-9], and to those of the other theories [3,4,10], which show good agreement. The conclusions are presented in Section 4.
Formalism
Anharmonic effective potential
To determine EXAFS cumulants of a semiconductor it is necessary to specify its interatomic interaction potential and force constant. Let us consider an anharmonic interatomic effective potential expanded up to the third order around its equilibrium
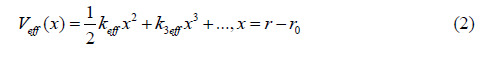
where keff is the effective local force constant, k3eff is the cubic anharmonic effective parameter giving an asymmetry of the anharmonic effective potential, x is the deviation of the instantaneous bond length r between two immediate neighboring atoms from its equilibrium value r0.
In the present theory the many-body task is simplified into the one of one-dimensional model with taking the many-body effects into account based on including the first shell near-neighbor contributions to the vibrations between absorber and backscattered atoms. Therefore, the anharmonic effective potential Eq. (2) defined based on an assumption in the center-of-mass frame of single bond pair of an absorber and a backscattered has resulted as
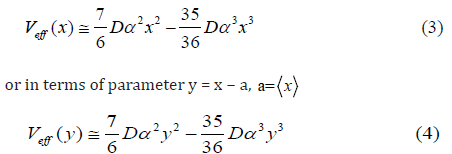
where α and D are Morse potential parameters describing respectively the width of the potential and the dissociation energy.
Here the effective local force constant and cubic anharmonic parameter for semiconductors included in Eq. (2) as the parameters of anharmonic effective potential have been defined and given in the following forms
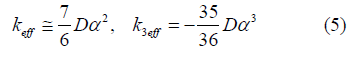
Note that in the derivation of the above expressions we consider the diamond structure, where each atom is bonded to four nearest neighbors and Morse potential is assumed to describe the single pair atomic interaction.
For further calculation of EXAFS cumulants using quantum thermodynamic perturbation theory in the present theory the anharmonic effective potential Eq. (4) is expressed in the sum of the harmonic contribution and a perturbation d V due to the weak anharmonicity in EXAFS as
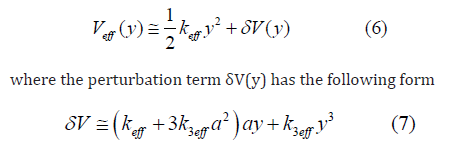
EXAFS cumulants
Derivation of EXAFS cumulants in the present theory for semiconductors is based on quantum statistical theory [11] and the anharmonic effective potential derived in the previous Section 2.1. Now we consider the physical quantity which is determined based on an averaging procedure using the canonical partition function Z and statistical density matrix ρ, e.g.,
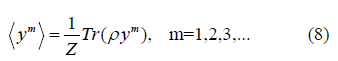
Atomic vibrations are quantized in terms of phonons, and anharmonicity is the result of phononphonon interaction, that is why we express y in terms of the annihilation and creation operators 
respectively
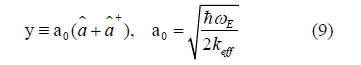
which have the following properties
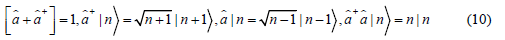
as well as use the harmonic oscillator state n as the eigenstate with the eigenvalue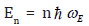 
respectively
Based on the local force constant given by the first equation of Eqs. (5), the correlated Einstein frequency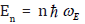 
respectively
Based on the local force constant given by the first equation of Eqs. (5), the correlated Einstein frequency ω E and temperature θE for semiconductors have resulted and given by
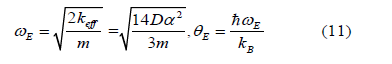
where kB is Boltzmann constant m is atomic mass (for monatomic crystal). The canonical partition function in Eq. (8) can be expressed as
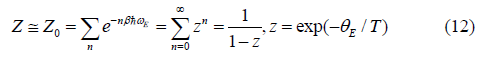
Using the above results for the correlated atomic vibration and the procedure depicted by Eqs. (8) - (12), as well as the first-order thermodynamic perturbation theory [11] the temperature-dependent EXAFS cumulants in the present theory for semiconductors have been derived.
Here, based on the procedure depicted by Eq. (8) we derived the even moment expressing the second cumulant or MSRD
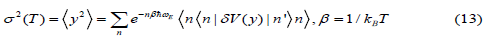
and the odd moments expressing the first (m = 1) and third (m = 3) cumulants
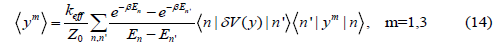
Where δV( y) is taken from Eq. (7) and the operations expressed by Eqs. (8) - (10) have been applied to calculate the matrix elements given in Eqs. (13) - (14).
Consequently, the EXAFS cumulants for semiconductors have resulted for the first cumulant describing net thermal expansion or lattice disorder
for the second cumulant describing MSRD
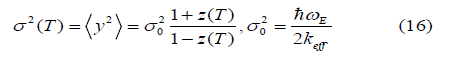
and for the third cumulant describing the mean cubic relative displacement (MCRD) or the asymmetry of the pair distribution function
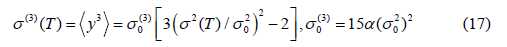
Here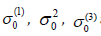 
are zero-point energy contributions to the Cumulants 
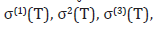respectively.
Hence, the EXAFS quantities given by Eqs. (15) – (17) have been described in terms of second cumulant. This is useful not only for reducing the numerical calculations but also for creating a method for obtaining the remain theoretical or experimental EXAFS quantities of the considered semiconductor based on only the calculated (theoretical study) or measured (experimental study) second cumulants.
Note that the derived cumulants describe the thermodynamic and anharmonic properties and based on Fourier transform magnitudes of EXAFS spectra described by Eq. (1) containing these cumulants contribute to accurate structural determination of semiconductors.
Numerical Results and Discussions
Now we apply the expressions derived in the previous sections to numerical calculations for temperature-dependence of EXAFS cumulants of diamond structure type semiconductor Ge using its Morse potential parameters [12] D = 1.63 eV, α = 1.50 Ǻ-1. The calculated values of the local force constant keff, anharmonic cubic parameter keff, correlated Einstein frequency ωE and temperature θE are written in Table 1.
Table 1: Calculated values of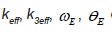 
of semiconductor Ge using its Morse potential parameters [12].
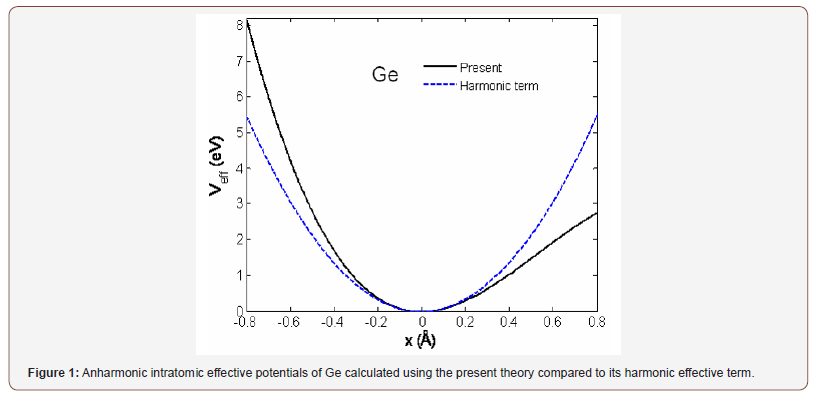
Figure 1 illustrates the anharmonic interatomic effective potentials of Ge calculated using the present theory. It is asymmetric due to the anharmonic contribution described by the third order parameter k3eff of the potential. Here, the anharmonic effective potential of Ge is compared to its harmonic effective term to show the rate of its asymmetry due to anharmonicity. This anharmonic effective potential of Ge is used for calculating the considered EXAFS quantities.
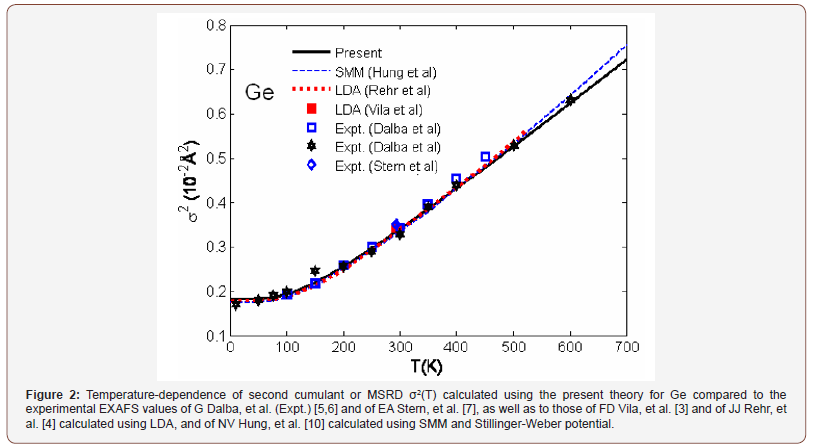
Temperature-dependence of second cumulant or MSRD σ2(T) of Ge (Figure 2) calculated using the present theory agrees well with the experimental values of G Dalba, et al. (Expt.) [5,6], and of AE Stern, et al. [7], with the result of FD Vila, et al. [3] and of JJ Rehr, et al. [4] calculated using the LDA (local density approximation), and of NV Hung, et al. [10] calculated using the SMM (statistical moment method) and Stillinger-Weber potentials.
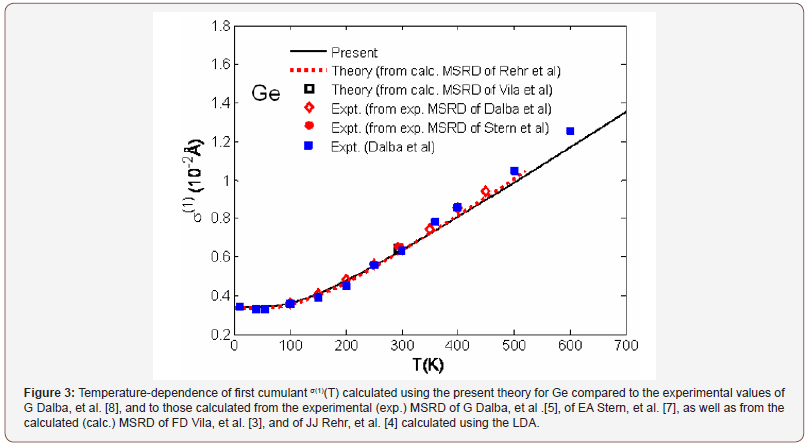
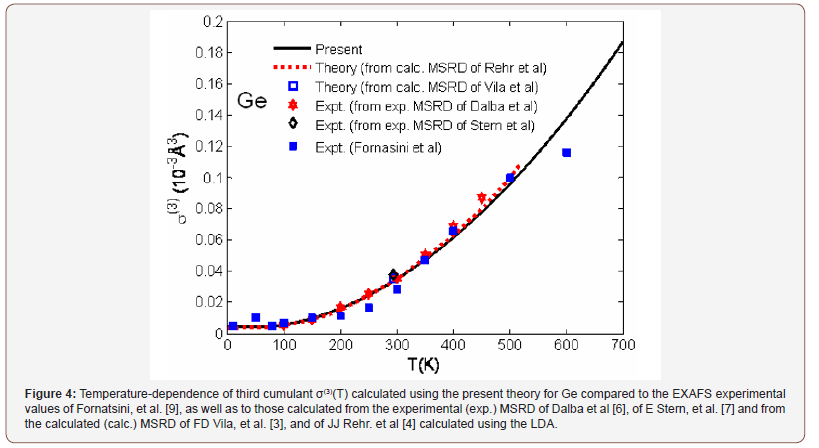
Temperature-dependence of the first cumulant or net thermal expansion σ(1)(T) of Ge (Figure 3) calculated using the present theory agrees well with the experimental values of G Dalba, et al. [8], and to those calculated from the experimental (exp.) MSRD of G Dalba, et al. [5], of EA Stern, et al. [7], as well as from the calculated (calc.) MSRD of FD Vila, et al. [3], and of JJ Rehr, et al. [4] calculated using the LDA. Such good agreement is also shown for the third cumulant σ(3)(T) of Ge (Figure 4) calculated using the present theory with the EXAFS experimental values of P Fornasini, et al. [9], as well as to those calculated from the experimental (exp.) MSRD of Dalba, et al. [6], of E Stern, et al. [7] and from the calculated (calc.) MSRD of FD Vila, et al. [3], and of JJ Rehr, et al. [4] calculated using the LDA.
Note that the good agreement of the values calculated from the theoretical and experimental second cumulants or MSRDs of Ge (Figure 2) for the first cumulants presented in Figure 3 and for the third cumulants presented in Figure 4 with experiment confirms not only their validity as the theoretical and experimental EXAFS quantities but also the possibility of getting the other EXAFS parameters if the second cumulants are calculated or measured. This actually also confirms the validity of the above created method which has been used in the present studies.
The above figures show that at high temperatures the first and second cumulants are linearly proportional to temperature T and the third cumulant to T2. They contain zero-point energy contributions at low-temperatures, a quantum effect.
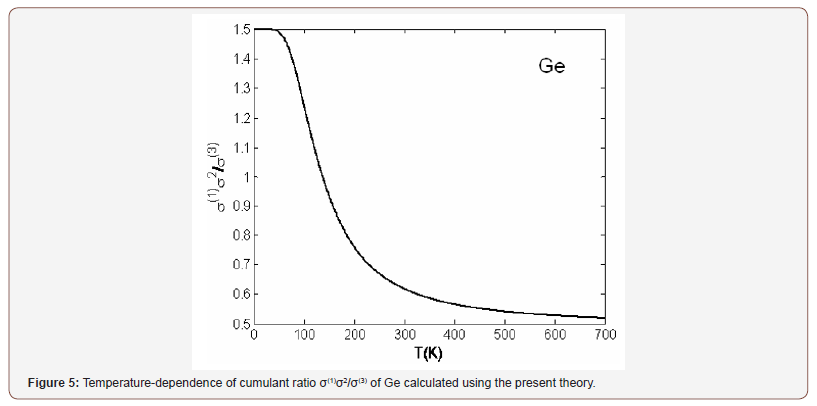
The cumulant ratios are often considered in the anharmonic EXAFS studies [2,13,14]. Figure 5 illustrates temperaturedependence of cumulant ratio σ(1)σ2/σ(3) calculated using the present theory for Ge. Here, σ(1)σ2/σ(3) approaches 3/2 at low-temperatures and the classical value [13,14] of 1/2 at high temperatures beginning from the Einstein temperature (θE = 363.26K for Ge, Table 1) as for the other crystal structures [2]. Hence, it remains to be considered as the standard for studying EXAFS cumulants of semiconductors calculated using the present theory.
Conclusion
In this work a theory has been derived for studies of temperature-dependence of DWFs of semiconductors presented in terms of cumulant expansion in EXAFS. They contribute to accurate structural determination, as well as to valuation of the thermodynamic properties and anharmonic effects accounting for the net thermal expansion, the MSRD, and the asymmetry of the pair distribution function of semiconductors.
The advanced studies are succeeded based on the further development of the ACEM derived primary for fcc crystals into the one applied to semiconductors. Here the many-body task is simplified into the one of one-dimensional model with taking the many-body effects into account based on including the first shell near-neighbor contributions to the vibrations between absorber and backscattered atoms.
The method created in this theory has the advantage that all theoretical and experimental EXAFS quantities are provided based on only the calculation (theoretical study) or measurement (experimental study) of second cumulants. It is useful not only for reducing the numerical calculations or measurements but also for creating a simple way of obtaining the considered quantities.
The theory is successfully applied to valuation of temperaturedependence of three first EXAFS cumulants of semiconductors. At high temperatures the first and second cumulants are linearly proportional to temperature T and the third one to T2. They contain zero-point energy contributions at low-temperatures, a quantum effect. The cumulant ratio σ(1)σ2/σ(3) expresses the same properties as those for the other crystal structures so that it remains to be considered as the standard for EXAFS cumulant studies of semiconductors.
The good agreement of the results calculated using the present theory and of those obtained by using the created method with experiment and with those of other theories for Ge having diamond structure illustrates the simplicity, advantage and efficiency of the present theory and the created method in the theoretical and experimental EXAFS studies of the thermodynamic properties and anharmonic effects of materials having any structure including semiconductors.
To read more about this article...Open access Journal of of Engineering Sciences
Please follow the URL to access more information about this article
To read more about this article...Open access Journal of of Engineering Sciences
Please follow the URL to access more information about this article
No comments:
Post a Comment