Authored by C Bastien
Abstract
In fatal pedestrian to vehicle collisions, accident investigators must attempt to reconstruct events that led up to the collision to determine liability in a court of law. In the absence of suitable video footage, the vehicle speed is calculated using particle-based throw distance calculators such as the Searle method. Until recently, no methods concentrated on the velocity of the crossing pedestrian, vital for determining responsibility. A new approach, the Pedestrian Crossing Speed Calculator (PCSC), which uses evidence left on the bonnet and windscreen along with pedestrian anthropometry to calculate a pedestrian crossing speed, has been proposed in a previous research, and validated against three real accidents where the pedestrian approach was orthogonal to the vehicle. The range of application of the PCSC theory is investigated in this paper. This study has considered 48 Finite Element simulations to further validate the PCSC against a saloon type and SUV vehicles. In the case of the saloon type, the PCSC theory for a pedestrian crossing approach angle <10°, i.e. a pedestrian crossing trajectory no longer perpendicular to the vehicle trajectory, has been fully vindicated. The study has also confirmed the PCSC hypothesis stating that for saloon vehicles the relationship between and increase in bonnet dent width was caused by an increase in pedestrian gait angle. The study also concluded that the PCSC theory was less conclusive in the case of SUV collisions. This paper confirms that PCSC is unique and can have an important role in the field of accident reconstruction and for law enforcement; with the potential to determine vehicle speeds from a known pedestrian crossing speed, which will allow the calculation of the vehicle velocity in the absence of physical evidence left on the road surface.Introduction
Pedestrian collisions are often tragic and sometimes even fatal events that happen all around the world. These events are caused by the pedestrian, careless driving or a combination of the two. The Police authorities are then responsible for gathering all the evidence leading to the fatal collision. Evidence can be found in multiple ways, like video footage (either CCTV or dashcam), data from the vehicle ECU, or if necessary, witness statements and physical evidence left on the road, such as skid marks. Pedestrian throw distance calculators such as Searle’s method can then be used with physical evidence to estimate the velocity corridor the vehicle was expected to be travelling in, although using this method, the crossing speed of the pedestrian cannot be ascertained. The Pedestrian Crossing Speed Calculator (PCSC) [1] is a new particle-based method of accident reconstruction that uses physical evidence left on the front end of the vehicle to calculate the crossing speed of the pedestrian. Not only this, but if the pedestrian crossing speed is known, then it can be applied in reverse to find the velocity of the vehicle.When a pedestrian impacts a vehicle, the first point of contact is between the bumper and knee [2,3]. After initial contact, the pedestrian rotates about the bonnet leading edge and hits the windscreen, the impact of which is offset laterally and longitudinally from first contact [4]. This head contact location is heavily influenced by two factors; the front-end geometry of the vehicle and the height of the pedestrian. A bonnet with a lower height leading edge carries the pedestrian further onto the vehicle [5] and a tall pedestrian is 17% more likely to hit the windscreen [6]. (Figure 1) shows an example of the pedestrian kinematics with different front-end geometries, using Madymo a pedestrian multibody computer model [1]. The Searle method is currently used in UK court proceedings, which is a particle-based mathematical model which uses evidence markers such as skin marks and pedestrian throw distance to calculate a vehicle velocity [8]. It has been shown to compare well to a collection of accident data, predicting vehicle velocities close to the known values [9]. Several deficiencies exist with this method. A constant friction coefficient of 0.7 is used, which is not representative of a change in road condition, i.e. dry (0.73), wet (0.67), icy (0.30) [10]. Differences in velocities between the pedestrian and vehicle at the moment of impact also require the use of a projection efficiency, which is dependent on vehicle front end geometry.
The Pedestrian Crossing Speed Calculator (PCSC) is a new forensic investigation tool that can be used to calculate the crossing speed of a pedestrian. It assumes the pedestrian to be a particle and uses vector algebra to determine a directional vector post-impact.
The basic theory of the PCSC is based on the ratio between two angles [1]
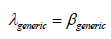
The first angle, λ, is the absolute angle of the pedestrian-vehicle velocity vector, which can be seen in (Figure 2). This vector is measured using two impact locations, the dent left on the leading edge of the bonnet by the pedestrian’s leg, and the dent left at the top of the bonnet or windscreen by the pedestrian’s head.
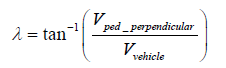
Equation 2 - Absolute angle of the pedestrian-vehicle compound velocity vector.
It is assumed in Equation 3 that the pedestrian is travelling on a path perpendicular to the vehicle’s direction of travel. This may not always be the case and so a non-zero approach angle between the pedestrian and vehicle can be observed. This change of angle is included in Equation 2, where α is the approach angle of the pedestrian. It should be noted that Equation 2 reverts to Equation 1 when the approach angle α is zero. The correction value is added to the vehicle velocity if the pedestrian is travelling towards from the car, and visa-versa.
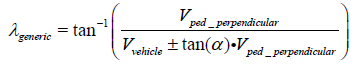
Equation 3- Absolute angle of the pedestrian-vehicle compound velocity vector with pedestrian approach angle included.
It should also be noted that there are multiple ratios of vehiclepedestrian velocities that can fulfil λ. The ratio of velocities however must be calculated from the impact evidence on the vehicle. The angle β is the head approach angle of the pedestrian between impacts of the leg on the bumper and head on the windscreen. Overly simplified, it is the angle between these two impact points. The lateral distance between these points is W, and the longitudinal distance between them is H. This can be observed in (Figure 3).
The angle β is therefore a function of W and H, however the pedestrian’s head may be offset from the leg impact location. This is captured in the term Γ_generic, and as such β can be calculated as per Equation 3.
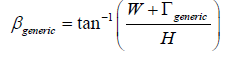
The head position relative to the leg impact location will be determined by anthropometric factors such as leg length, and the condition of the pedestrian pre-impact. This condition is based on the hip gait angle of the pedestrian, θ. The distance between the bonnet impact location and the pedestrian’s head will be larger than for a wider pedestrian stance, and near zero for a standing stance. (Table 1) summarizes the maximum hip gait angles for a given stance. It must be noted that this does not divulge the crossing speed. For example, a pedestrian crossing at running speed can have a running gait, as well as a standing or walking gait depending where in their stride they are at impact.
If the pedestrian’s head is forward of the bonnet impact point, the head approach angle β will be smaller than λ. If the pedestrian’s head is trailing the bonnet impact point, then β will be greater than λ. This is illustrated in (Figure 4). Equation 4 shows Γ_generic, which depends on the pedestrian condition pre-impact, i.e. width of pedestrian gait, anthropometrics etc.
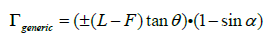
The distance Γ_generic is illustrated in Equation 5, where L is the pedestrian leg length, F is the height of bumper impact, θ is the pedestrian gait width and α is the approach angle of the pedestrian to the vehicle. These pedestrian measurements can be seen in (Figure 5).
Combining the full equations for λ and β produces Equation 6:
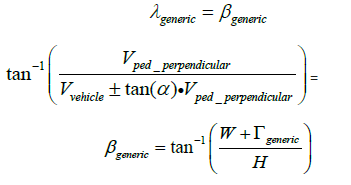
The PCSC has already been verified [1], using data from three real collisions to show the PCSC can predict velocities consistent with the findings of the UKPF. These collisions all occurred with an approach angle α, of 0° and has been highlighted by the authors as a limitation of this verification.
This paper will attempt to further validate the PCSC by running FE simulations using the THUMS4.01 human body model and assess the extent of usefulness on the PCSC theory. The Latest computer human body technologies involve finite element model (THUMS and GHBMC [13]). These models are designed to replicate the physical properties of the human body and are based on the results of many studies and CT scans [1]. It has been proven that THUMS can predict the dynamic impact and response compared to a PMHS to within ±15% [14,15]. THUMS has also been validated for post impact kinematics, producing results consistent with the Searle method at speeds up-to 40km/h [15].
To read more about this article.. Open access Journal of Global Journal of Forensic Science & Medicine
Please follow the URL to access more information about this article
https://irispublishers.com/gjfsm/fulltext/numerical-validation-of-the-pedestrian-crossing-speed-calculator-pcsc.ID.000525.php
To know more about our Journals....Iris Publishers
To know about Open Access Publishers





No comments:
Post a Comment