Authored by Mekonnen Tilahun
Abstract
The annual Ethiopian goat meat and mutton production is very low. Major causes contributing to such low meat production include slaughtering animals at immature body-weights, poor genetic potential of the local breeds, poor feeding conditions and policy issues. Increasing the current level of productivity is essential to provide meat to the ever-increasing human population and to satisfy the huge demand of live-animal export to neighboring countries. Ethiopian Sheep and Goat Productivity Improvement Program has imported Dorper sheep and Boer goat from South Africa to cross with local sheep and goats for the purpose of upgrading the productivity of local breeds. In order to promote the merit of such crossbreeding activities it is important to have data on growth potential characteristics. Accordingly, the objectives of this study was to apply linear mixed model for evaluating body-weight gain of pure and crossbred lambs and test their difference in weight gain. A linear mixed model was used to analyze repeated data on boy-weight obtained from three breed-groups, i.e., Pure Central Highland Sheep, 50%Central Highland Sheep 50%Dorper Sheep, and 75%Central Highland Sheep 25%Dorper Sheep. The pure Central Highland Sheep show a significantly lower body-weight gain than the two crossbreds. This increased body-weight gain of the crossbreds in comparison to Central Highland Sheep is justified by the higher blood-level of the crossbreds and their ability to efficiently utilize the feeds as compared to the Central Highland Sheep. This result suggests the impact of cross breeding on increased body-weight gain and thereby increasing meat production of growing lambs.Keywords: Body-weight gain; Breed-group; Covariance structure; Model selection
Introduction
Human population growth in Ethiopia is forcing the conversion of many former grazing areas into cropland needs for increased food production. Raising ruminants is becoming increasingly difficult as a result of shortage of grazing areas. The annual Ethiopian goat meat and mutton production is 67580 and 86500 tons, respectively for goats and sheep which contributes 16.98 and 21.73% of the total ruminant livestock meat output [1]. Annual meat production is estimated 8–10kg per sheep and goats slaughtered. A major cause contributing to such low meat production is that animals are commonly slaughtered at immature body weights, 16–20kg [2]. The low level of production is also due to another constraint namely poor genetic potential of the local breeds, poor feeding conditions and policy issues [3].Increasing the current level of productivity is essential to provide meat to the ever-increasing human population, to satisfy the huge demand of live-animal export to neighboring countries and to raise earnings and household incomes of smallholder farmers [4,5]. According to Momani et al., 2010 and Singh and Acharaya, 1982 two alternative methods of production development exist: using the knowledge of genetics (selection of local breed and cross them with exotic breeds) and improvement of environmental conditions (management, feeding and health care). Ethiopian Sheep and Goat Productivity Improvement Program (ESGPIP) has imported Dorper sheep and Boer goat from South Africa for crossbreeding purpose to upgrading the productivity of local breeds in the country. In order to promote the merit of such crossbreeding activities it is important to have data on growth potential characteristics and evaluate animals accordingly. Performance evaluation of pure and crossbred lambs will provided vital information that demonstrates opportunity for the genetic improvement of production performance under specific feeding and management conditions [6].
Accordingly, the objectives of this study was to apply linear mixed model for evaluating body-weight gain of pure and crossbred lambs and test their difference in body-weight gain.
Materials and Methods
Description of the study area
This study was conducted on station at Sirinka agricultural research center which is located 508 km away from Addis Ababa. The site is located at an altitude of 1850 m.a.s.l and at 110 451 0011N and 390 361 3611E. The rainfall pattern is bimodal, with two-rainfall season, belg (February - April) and meher (July – November) and the mean annual rainfall amount is on average about 950 mm. The area is a moderate warm temperature zone with mean daily temperature ranges from 16-21 °C.Experimental animals and their feeding
Based on their blood-level, the experimental ram lambs for this study consisted of three breed-groups, i.e., I: pure (local) Central Highland Sheep (CHS), II: 50%CHS50%Dorper Sheep, and III: 75%CHS25%Dorper Sheep. For each of the three breed-groups, nine growing lambs were available. The pure CHS were purchased from the local markets in the study area. The 50%CHS50%Dorper were obtained from Sirinka agricultural research center farm and the 75%CHS25%Dorper were purchased from farmers participating in sheep and goat improvement program respectively.The animals used were of similar size, young age and sound health conditions. The ages of the animals were obtained from farm record data of Sirinka agricultural research center while the remaining breed-groups age was estimated through interviewing farmers and observing dentition. The ages of the animals were thus in the range of 3 to 5 months.
Before the beginning of the experiment, animals were dewormed and sprayed against internal and external parasites and brought indoors after the pens had been properly washed and disinfected. They were individually housed in individual cages with removable feeders and water troughs.
Experiment animals had free access to water, and were allowed ad libitum intake of the native grass hay but with restricted amount of concentrate mixture considering 2% of their body-weight on dry matter basis which were adjusted every ten days following regular weight measurement of the animals. The native grass hays were chopped to pieces to encourage intake. Concentrate mixtures (i.e., noug seed cake, wheat bran, crushed sorghum grain and common salt with a proportion of 46%, 28%, 24% and 2%, respectively) was formulated before the start of the experiment by using Winfeed 2.84 software program and it was given twice daily at 0800 h and at 1400.
Table 1: Experimental breed-groups.
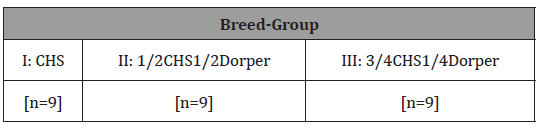
The experiment lasted for 90 days from July to October 2011. The table below describes these arrangements (Table 1).
Body-weight measurements
Following a 14-day acclimatization period, each growing lamb was weighed at the beginning of the experiment (initial bodyweight, IBW) and every successive ten-day thereafter. All lambs were weighed during morning hours after overnight fasting using suspended weighing scale having sensitivity of 50 grams.Statistical Methods
SAS-program version 9.4 (SAS 2015) was used for all statistical analysis in this study.Modelling approach
In this study, for analyzing the data on repeated records of bodyweight gains using linear mixed model, dependencies between repeated body-weight gains of a lamb have to be modelled. In order to realize this, lamb-specific random regression coefficients al0 – aln are introduced.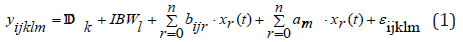

PROC MIXED DATA=SHEEP METHOD=REML;
CLASS Breed Diet DT LAMB;
MODEL BWG = Breed DT IBW X1(Breed) X2(Breed) ...Xn(Breed) /NOINT;
RANDOM INT X1 X2 ... Xn/SUBJECT=LAMB TYPE=UN;
If n=0 in model (1), this means that one random effect per lamb is included and that the covariance function in (2) is of the form:
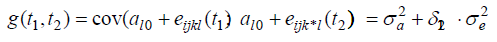 Here, 12 1 2 δ = 1 for t = t ; in all other cases, 0 12 δ = .
Because of the above formula, all pairs of measures on the same
lamb have the same correlation. Thus, the correlation between two
measures at time t1 and t2 is:
Here, 12 1 2 δ = 1 for t = t ; in all other cases, 0 12 δ = .
Because of the above formula, all pairs of measures on the same
lamb have the same correlation. Thus, the correlation between two
measures at time t1 and t2 is: Up this point, the covariance structure has been modelled by using lamb-specific random effects only. In the following, the residual covariance structure of model (2) will be extended further [7,8].
Let e(t) be the residual effect of a lamb for the body-weight gain on days-on-test of t. Then, let us use the following model: e(t) = e1(t) + e2(t). Here, e1(t) stands for the component of the serial correlation between repeated measurements for a lamb,e2(t) denotes the component for the residual error with an equal variance for all measurements. The residual effects for the latter are assumed to be independent and identically distributed. The model for the serial covariance structure is completed by adding a distance correlation function g. This function is selected in such a way that all residual effects e1(t) of a lamb have the same variance and that the correlation between two such effects is always positive but decreases monotonically with increasing temporal distance between two measurements for the same lamb. Then, the variance and covariance function of the residual effects of a lamb are given by:
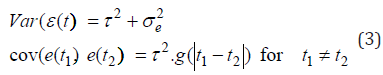

PROC MIXED DATA=SHEEP METHOD=REML;
CLASS Breed DT LAMB;
MODEL BWG = Breed DT IBW X1(Breed) X2(Breed) ...Xn(Breed) / NOINT;
RANDOM INT X1 X2 ... Xn/SUBJECT=LAMB TYPE=UN;
REPEATED/SUBJECT=LAMB TYPE=SP (EXP) (DT);
Once the optimum model for the covariance structure is found, then tests of fixed effects for the different breed-groups can be done with the help of t- and F-tests (Tukey-Tests) [9-12].
Results and Discussion
Descriptive statistics
A summary results of the data on body-weight gain over the different sub-periods, i.e. from day 10 (t10) up to day 90 (t90) for the different breed-groups, is given in the table below (Table 2).With repeated measures data, an obvious first statistics to consider is descriptive statistics results of body-weight gain of animals against time. Table 2 shows among others the means and standard deviations for individual ages at recording in 10-days intervals. Generally, the mean and standard deviations of the data in the above table increased slowly and steadily with age. This pattern of increase in mean and standard deviation over time could be explained in terms of the variation in growth rates of the different breed-groups [13-15].
To read more about this article....Open access Journal of Agriculture and Soil Science
Please follow the URL to access more information about this article
https://irispublishers.com/wjass/fulltext/analysis-of-growth-performance-data-in-sheep-using-linear-mixed-model.ID.000541.php
To know more about our Journals....Iris Publishers
To know about Open Access Publishers





No comments:
Post a Comment