Authored by Arif Hasnat*
Abstract
Compaction parameters determination in the laboratory require considerable time and effort that can be saved by using empirical correlations at the early stages. This paper introduces some efforts to predict the compaction properties of soils using the index test results. Apart from the experimental result, the result from other literature have also been considered in the analysis here. Different statistical investigation such as histogram, ACF, PACF, kernel function, correlogram and cross correlogram are used to find the relationship of liquid limit, plastic limit and plasticity index with optimum moisture content and maximum dry density. Regression analyses are done with support vector machine algorithm. The best R squared value found from the predicted equation is 0.86 for optimum moisture content and 0.91 for maximum dry density.
Keywords: Prediction; Optimum moisture content; Maximum dry density; Compaction parameters; Support vector regression
Introduction
During the construction of earthworks, filed compaction is important process. Compaction is a dynamic process by means of which soil particles are brought closer together by providing compactive effort leading to an increase in shear strength, reduction of compression and soil permeability. The two parameters which are determined in the laboratory by conducting either standard proctor or modified proctor test are the determination of optimum moisture content (OMC) maximum dry unit weight (γdmax). These parameters are employed in the project specifications to monitor the relative compaction demands. The objective of this paper is to determine the correlations of index properties of soils with optimum moisture content and maximum dry density. Many research efforts have been conducted to correlate the soil index results with their compaction properties i.e. OMC and MDD mainly for clayey soils. Rowan & Graham [1] correlated gradation, specific gravity and shrinkage limit to compaction characteristics. Later Davidson and Gardiner omitted the specific gravity from the equation of Rowan & Graham [1] and included a plasticity index. Ramiah et al. [2] correlated only Liquid Limit with both OMC and MDD. Korfiatis & Manifopoulos [3] introduced four empirical factors in their correlation which was a function of the slope of the grain size curve correlating the MDD of granular soil to specific gravity and fine content of soils. Besides, according to Omar et al. [4], the most significant impact on the soil compaction properties is specific gravity. They studied the compaction characteristics of granular soils in the United Arab Emirates. on a data bank of 354 soil samples from different sources. In a few latest research’s efforts have been taken to create empirical models for the prediction of the compaction properties of ground grain soils. For finely grained soils, efforts have mainly been produced to correlate γdmax and OMC with either LL or PL in particular. Special emphasis has been given on compaction energy in a few studies.
Sivrikaya [5] correlated compaction characteristics of finegrained soils to their plastic limit (wP) as follows:
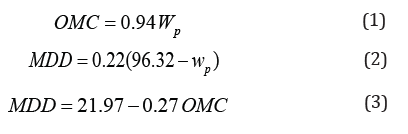
Sridharan & Nagaraj [6] developed the correlations given in Eq. 4 and Eq. 5
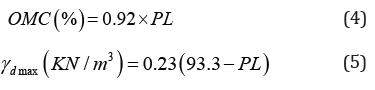
Gurtug &Sridharan [7] introduced CE in prediction of OMC and MDD shown in Eq. 6 and Eq. 7
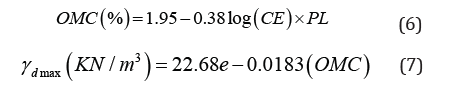
Eq. 8 and Eq. 9 are found from Faizah K [8],
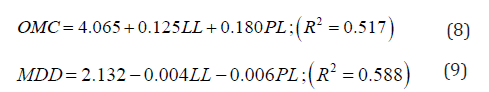
Mohd Ruslan [9] proposed Eq. 10 and Eq. 11

Noor et al. [10] added specific gravity in prediction of OMC and MDD shown in Eq. 12 and Eq. 13

In recent decades, modeling and problem of different geotechnical issues have been widely solved by artificial neural networks [11]. Gu¨naydın [12] used 126 test results of nine different soil types and used multi-linear regression method and ANNs method for the prediction of compaction parameters. Regression analysis and an estimated artificial neural network have shown powerful correlations (0.70–0.95) between soil classification and compaction parameters. There have been limited efforts to correlate − in combination with the PL or plasticity (PI)- γdmax and OMC with LL in the domain. Those works consist of these two parameters in combination (Eq. 8, 9, 10, 11) have relatively low R squared value. In this paper, the regression analysis is done with support vector machine algorithm and thus those error is reduced in a threshold limit. The original SVM algorithm was invented by Vladimir N Vapnik & Alexey Ya Chervonenkis [13]. In 1992, Bernhard E Boser, Isabelle M Guyon and Vladimir N Vapnik suggested a way to create nonlinear classifiers by applying the kernel trick to maximummargin hyper-planes. It is a very popular method and the aim of this model is to find a special straight line for discriminating different classes. For drawing a line between two classes, there are a lot of opportunities and Support Vector Machine (SVM) tries to find the ultimate line of both cases. A boundary line in which SVM is near is tried to be found to distinguish the binary classes from each other. After the boundary line is found, using training data, test data are classified according to which side of the border. The samples are moved to a higher dimensional space which cannot be linearly discriminated. It is now practiced in different field for linear and non-linear regression analysis. Osman Günaydın [14] shown that the compaction parameters can be predicted using support vector regression.
To read more about this article.. Open access Journal of Current Trends in Civil & Structural Engineering
To know more about our Journals....Iris Publishers





No comments:
Post a Comment