Authored by Mohammadreza Akbari*,
Abstract
In this article, we want to solve an analytical nonlinear partial differential equation that it is very applicable in all fields of engineering and basic sciences. This kind of nonlinear partial equations is used extensively in most engineering fields including chemical, mechanical, civil, electrical, and other engineering. As all experts know most of engineering actual systems behavior in practical are nonlinear process and analytical scrutiny these nonlinear problems (especially nonlinear analytical solution of partial equations) are very difficult or sometimes impossible. Our purpose is to enhance the ability of solving the mentioned nonlinear partial differential equations at engineering fields with a simple and innovative approach which entitled ‘’Akbari-Sara’s Method’’ or ‘’ASM’’.
Keywords: Akbari Sara’s Method (ASM); Nonlinear partial differential equation; Analytical solution; Eigenvalues; Shape function
Introduction
Partial nonlinear differential equations which arise in real- world physical problems are often too complicated to be solved exactly [1,2]. And even if an exact solution is obtainable, the required calculations may be too complicated to be practical, or it might be difficult to interpret the outcome. In fact, solving nonlinear equations can guide researchers to comprehend the physical phenomena deeply and sometimes leads them to investigate some facts which are not easily understood through common observations [3,4]. Based on the above explanations, here we aim to discuss nonlinear partial differential and the behavior of the physical its. In this literature, we have a governing equation for studying nonlinear behavior in engineering processes and solving it analytically with a new approach like AGM, Akbari Ganji Method [5-10]. This method is called the abbreviation ASM (Akbari Sara’s Method), which can easily solve all nonlinear problems in case analytical and is very simple and flexible. Other methods [11] compared to ASM do not have this ability to gain the solution of the presented problem in high precision and accuracy so nonlinear differential equations such as the presented problem in this case study should be solved by utilizing new approaches.
Application
We consider an unsteady state of nonlinear partial differential equation with constant physical coefficients that depends on the engineering process. The constant values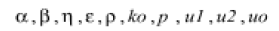 
depend on what field of engineering we want to solve this equation. For example, these constant values in mass transfer, heat and fluid transfer, electrical circuits, as well as in beam-column equations are defined respectively in chemical engineering, mechanical engineering, civil engineering and electrical engineering and all engineering fields.
The governing nonlinear partial differential equation of engineering fields is expressed as follows:
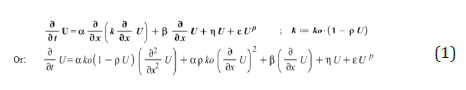
Boundary and initial condition:
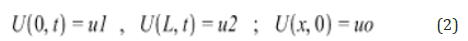
We separate equation Eq. (1) from steady and unsteady state as follows:
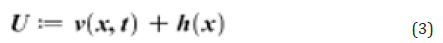
After separation, the result is given by the following two differential equations:
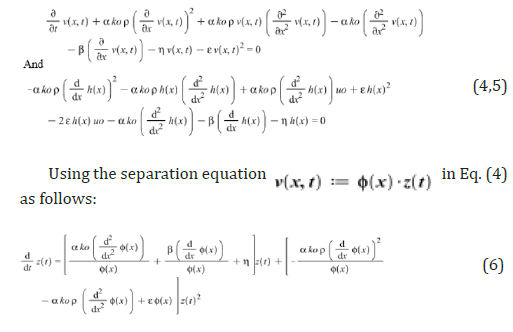
The coefficient z(t) in the Eq. (6) can derive the following differential equation for calculating eigenvalues λ and its function
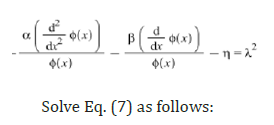
And boundary conditions:
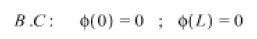
The constant coefficients _C1, C2 are obtained from Eq. (8) and given the homogeneous boundary condition with forming the coefficients matrix for the homogeneous equation as follow:
The parameters of Eq. (10) are as follows:
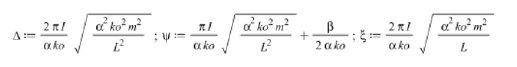
By selecting the physical values as follows:
Using the orthogonality of the modes of the function φ(x) in Eq. (6), we can obtain the following:
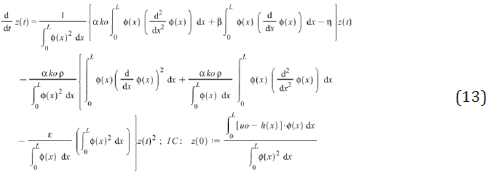
After substituted the physical values Eqs. (12) and the eigenvalue function Eqs. (10,11), and solving it by ASM method Eq. (13), the following is obtained:
Comparing the Achieved Solutions by Numerical Method and ASM (Akbari Sara’s Method)
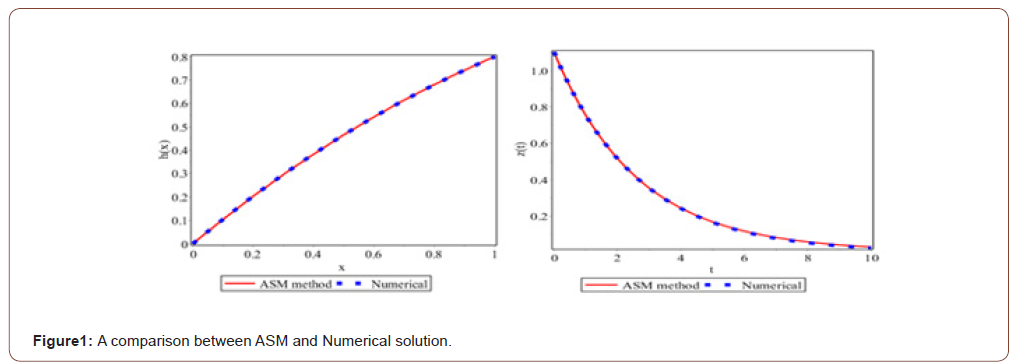
(Figure 1) And finally the solution of the nonlinear partial differential Eq. (1) is solved analytically by ASM method as follow:
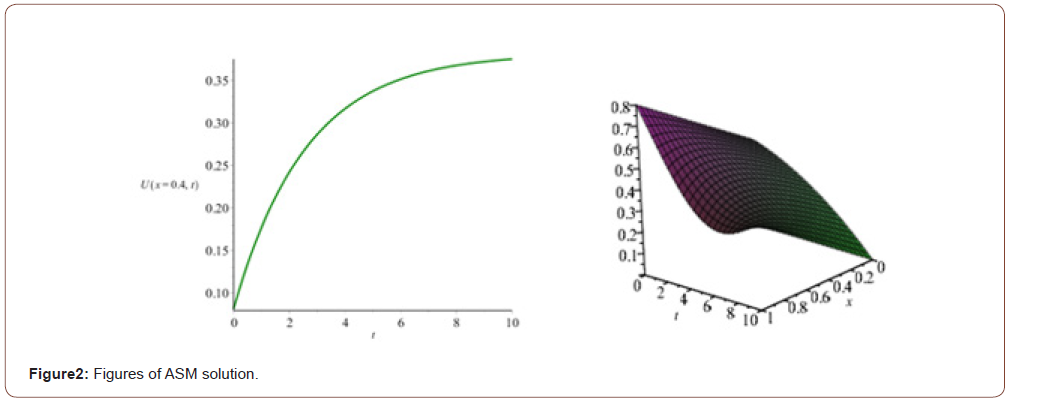
The diagram of the place-time is as follows: (Figure 2)
Conclusion
In this paper, one complicated nonlinear partial differential equation has been introduced and analyzed completely by Akbari- Sara’s Method (ASM) and also the obtained results have been compared with Numerical Method (Runge-Kutte 4th). A modern method (ASM) for solving all kinds of complicate nonlinear partial differential equations in engineer field and basic science which can be PDEs, or ODEs has been presented.
To read more about this article....Open access Journal of Biomedical Engineering & Biotechnology
Please follow the URL to access more information about this article
To know more about our Journals...Iris Publishers
No comments:
Post a Comment