Authored by Mergen H Ghayesh*,
Abstract
In this brief review article, the effects of Saffman force in inertial microfluidics-based systems are discussed and investigated. A short discussion regarding the applications of microfluidics, especially inertial microfluidics, is given. Then, the importance of the present investigation is illustrated. The Saffman force is mathematically formulated based on matched asymptotic expansion approach. Moreover, the physical concept of this lift force is discussed in this analysis. Finally, the influences of various physical and material parameters on the Saffman force are investigated.
Keywords:Inertial microfluidics; Ultra-small particles; Saffman force; Inertial migration
Introduction
Small-scale electromechanical devices have a great potential to revolutionize many existing fields of technologies [1]. A wide range of promising applications of these devices has recently been reported. These applications include but not limited to cell manipulation, energy harvesting, structural reinforcements, cancer diagnosis, mass sensing and drug delivery [2-5]. Smallscale electromechanical devices [6,7] are generally fabricated using microscale/nanoscale structural components involving microscale/ nanoscale beams [8-20], plates [21-28] and shells [29,30] as well as nanotubes [31-33] and fluid-conveying nanotubes [34-36]. For more information on microscale/nanoscale structural components, a reader is referred to review papers [37,38]. Similar to large-scale structures [39-41] in which geometric nonlinearity is likely [42- 48], for analyzing these components, large deformation effects are important. Last 20 years have seen a dramatic increase in the number of research studies and investigations on the mechanical and physical behavior of structural components [49-52] at smallscale levels [53,54].
One of important small-scale electromechanical devices is microfluidics, which deals with the manipulation and control of fluids and particles at microscales. This novel type of ultra small devices has extensively been used for various purposes by researchers and engineers [55,56]. For instance, in an exciting investigation by Shafiee et al. [57], using microfluidics-based technology, an acute portable biosensor was invented for detecting the human immunodeficiency virus (HIV). Furthermore, Warkiani et al. [58] fabricated a microfluidics-based device of a spiral geometry for detecting the circulating tumor cells in human blood; they showed that this technique of detection was relatively inexpensive, label-free and fast.
In addition to these fascinating applications, inertial microfluidics has lately been utilised for malaria detection [59].
Inertial microfluidics, in which the geometry and internal forces play a critical role, belongs to the passive type of microfluidics. Due to comparatively low costs, simple design and high efficiency, the popularity of inertial microfluidics among scientists and researchers has dramatically increased in recent years. In the channel of inertial microfluidics, there are a number of various internal forces such as drag, wall-induced, and Saffman. In this brief review paper, the influences of Saffman force on ultrasmall moving particles in inertial microfluidics are focused. The concept of Saffman force is firstly discussed, and then a number of mathematical relations are given to formulate this force. The effects of different parameters on the Saffman force are lastly investigated.
Saffman Force
One phenomenon, which is commonly observed in many inertial microfluidics-based systems, is inertial migration. In this phenomenon, particles with a random initial distribution travel laterally to an equilibrium state during their direct movement in the channel. Let us take into account a straight microtube conveying fluid with particles. The microtube radius is denoted by R in this study. The equilibrium state of particles in this tube is 0.6R. This inertial migration is highly related to wall effects. Generally, the wall of the channel of an inertial microfluidics causes two main effects. The first effect is that the presence of a wall causes a fluid velocity gradient. The second effect is particle retardation, which is associated with the microfluidics wall. In this short discussion, we focus on the first wall effect only.
A microfluidics wall leads to a gradient in the fluid velocity profile (i.e. shear rate), and this consequently results in a lateral lift force on particles. This lift force is technically called “Saffman force”. Figure 1 depicts a spherical ultrasmall particle in a fluid flow with a constant velocity gradient (i.e. simple shear flow). Through use of matched asymptotic expansion approach, the Saffman force (Fs) on this particle is determined as
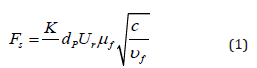
in which dp, Ur and K are respectively particle diameter, relative speed and Saffman constant. cg, μf and υf denotes the velocity gradient, fluid viscosity and kinetic viscosity, respectively. The Saffman constant is taken as 81.2. There are a number of assumptions and simplification for obtaining Eq. (1). For more detail on that interested readers can refer to Refs. [60] and [61]. It is worth mentioning that the kinetic viscosity is associated with fluid viscosity by υf = μf/ρf where ρf is fluid density. It is important to note that the magnitude of relative speed between the particle and fluid determines the force direction. As indicated in Figure 1, the Saffman force is exerted towards the region in which there are higher relative speeds. The magnitude of the relative speed is simply obtained by the following relation
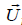P and 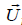f , respectively, represent particle and fluid velocities.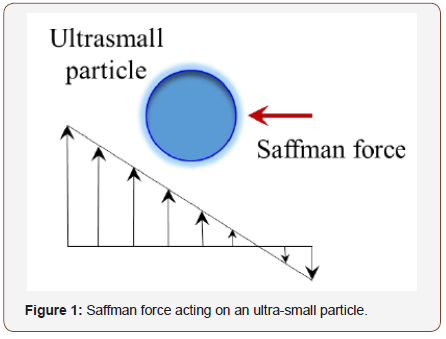
From Eq. (1), it is found that the Saffman force depends on a number of geometrical and material parameters such as fluid viscosity, particle diameter, and speed gradient. As the diameter of the ultra-small spherical particle increases, the Saffman force sees a noticeable increase in its magnitude. Furthermore, increasing the relative speed (Ur) leads to a proportional increase in this force as well. However, the rate of this increase in the Saffman force is considerably less than that of particle diameter according to Eq. (1). Another important parameter for the Saffman force is velocity gradient. Higher velocity gradients result in slightly higher Saffman forces.
Conclusion
The Saffman force induced due to the speed gradient in a simple shear flow has been discussed. A mathematical framework was reviewed so as to theoretically analyses the Saffman force in inertial microfluidics-based systems. Finally, the effects of a number of physical and material parameters on this lift force were discussed based on the given mathematical relationships. It was concluded that the particle diameter has an important increasing impact on the Saffman force. Moreover, the Saffman force proportionally increases with increasing the relative speed inside the inertial microfluidics. Furthermore, when the speed gradient increases, the Saffman force gradually becomes larger.
To read more about this article...Open access Journal of of Engineering Sciences
Please follow the URL to access more information about this article
To know more about our Journals...Iris Publishers
To know about Open Access Publishers
No comments:
Post a Comment