Authored by Ramalingam Shanmugam*
Abstract
In this article, we untangle the mystic of globally scaring corona virus (also, recognized as COVID 19). For this purpose, we define and utilize the index of dispersion to construct a new methodology based on the corona incidence rate, θ and a restriction parameter, β via an incidence rate restricted Poisson (IRRP) model for the data analysis. The IRRP model was introduced by Shanmugam [1] for another purpose and it is found to be quite suitable to understand the mystic nature of non- quantifiable restriction(s) imposed on the corona exposure/treatment in China and everywhere in the world as it appears. The publicly available [2] corona data as of 27 February 2020 in the World Health Organization’s (WHO) web page are analyzed and interpreted in this article. In specific, the new methodology detects non-trivial patterns not only in corona incidences but also in the restrictions imposed to deal with the pandemic like this corona virus and this discovery would have been obscured otherwise. The healthcare policies with respect to corona incidences should be congruent to much needed restrictions such preventive hygienic practices as minimal necessities but can go as far as isolation in quarantines as the data evidences enlisted in this article are providing a strong support for them.
Keywords: Incidence Rate; Index of Dispersion; Poisson Distribution; Odds Ratio; Restriction Level; Reduction Level; Tail Value at Risk; Vulnerability.
The background of this globally scaring corona virus is the following. On 24 January 2020, 1287 humans with corona virus (also recognized as 2019-Covid 19) were first noticed in Wuhan, China causing 41 deaths [3]. Neither the cause for the globally scaring corona virus nor an effective drug or treatment seems to be available. It appears (not proven) that the incubation period is speculated to be 7 to 14 days for those who have been exposed to the others. Now, this deadly virus has spread from China to other countries in Asia, Australia, New Zealand, Africa, Europe and American continents (Figure 1). The number of deaths due to corona virus in countries are mapped in Figure 2 and it has been changing on daily basis since 31st January 2020. See www.who.org for daily reports. The mystic corona cases have been a nightmare to the general public, health professionals, and the governing agencies globally.
The deadly epidemic like corona virus is not new to the world. The world citizens experienced a severe acute respiratory syndrome called SARS-CoV in year 2002 in Guangdong, China, MERS-CoV in year 2012 in the Middle East. As of 24 January 2020, there were 800 reported corona cases with a mortality rate of 3% (www.promedmail.org) [4,5,6] for data and background scenarios for the emergence and spread of the corona virus.
Noticing an occurrence of 12, 307 corona cases with a death of 259 as of 1 February 2020 in several countries around the world, the World Health Organization (WHO) [7] warned that incidence of corona virus is a global emergency. See Figure 1, an awareness of the corona incidences in countries, according to the WHO. See Figure 2 for statistics about the number of deaths due to corona virus.
Mediterranean, Conf= Confirmed, Susp=Suspected, EC=Exposed in China, EOCC=Exposed outside of China and the
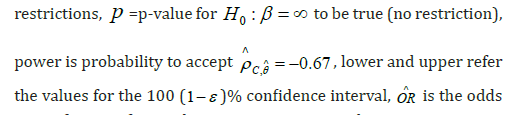
ratio of corona free under restriction compared to no restriction, R is the reduction in hazard rate of corona cases by the restrictions, V refers the vulnerability to corona virus in the region, and C denotes change in tail value at risk to corona virus due to imposed restrictions. Notation na refers not estimable because of zero variance or zero mean.
Main Contribution: A New Methodology
Let Y = 0,1, 2, 3,..... be a random number of corona cases of a specified type (which might be due to exposed to a carrier in a location) with an unknown incidence rate 0 <θ < β , where β denotes a non-observable (that is, latent) preventive or treatment action(s). Because the random variable (RV) Y is an integer valued Poisson type, we could consider the incidence rate restricted Poisson (IRRP) model
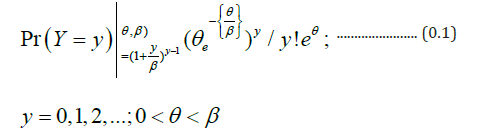
The IRRP in (0.1) was introduced by Shanmugam [1]. The IRRP is quite versatile and appropriate for the corona virus data analysis because there is an apparent restriction on the incidence rate, though data on the restrictions are neither collected nor reported in any place. In the absence of any relevant data on restrictions on the diagnostic, on how many days the infected individuals are quarantined, or on any preventive measures to stop the emergence of new cases etc., it is prudent to assume them as latent phenomena and it makes to treat them as a parameter, β .
In the absence restrictions, the incidence rate θ > 0 could be a parameter of the Poisson chance mechanism. That is, the probability of noticing one corona case in an infinitesimal interval of unit time is θ , while the probability of having two or more corona cases in that time interval is negligible. That is the framework of Poisson chance mechanism. It is not this way the corona incidences are happening.
In other words, only when there is no finite restriction on the incidence rate (that is, parameter β = ∞ ), the
model suits the commonly practiced Poisson chance mechanism, whose model is
See Stuart [8] for properties of the commonly utilized Poisson distribution. One such properties is the equality of the expected value and the variance. Otherwise (that is when the chance mechanism in which the corona incidences are quite restricted), the IRRP in (0.1) suits the reality of the corona incidence pattern.
We define here the ratio of the expected value over the variance is known as index of dispersion (ID) and it is useful in statistical modelling. The ID for Poisson mechanism of is value one because the equality of mean and variance characterizes the Poisson situation. Otherwise (that is, when the incidence rate is restricted with β ≠ ∞ , the ID for the IRRP in (0.1) is
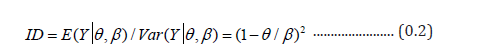
which attains a value in the domain[0,1] because θ ≤ β , suggesting that a characteristic property of the IRRP is under dispersion. In this article, we utilize the sample estimate of the index of dispersion,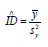 
as a basis to devise a simple alternative test to the Shanmugam’s C(α ) test, which was a bit cumbersome. See Shanmugam [9] for statistical applications of under, equal, and over dispersions.
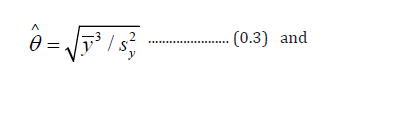
The maximum likelihood estimate (MLE) of the incidence rate and its restriction parameter involves the sample mean,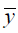 
variance, 
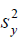as shown in (0.3) and (0.4) respectively. The MLEs are asymptotically most efficient [8]. A virtue of the MLE is that the MLE of a function of the parameters is the function of the MLEs. That is, the MLEs are
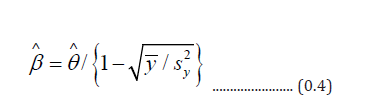
Be assured that in the Poisson chance mechanism, the sample
variance,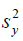 
and sample mean, y are likely to be not significantly different from each other. Consequently, the estimate in (0.3) becomes 
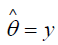confirming the (unrestricted) Poisson incidence rate is the sample average. In a restricted Poisson chance mechanism, the estimate in (0.4) quantifies the impact level of all restrictions. The sample mean and variance are independent only if the sample is drawn from the normal population. Otherwise, the sample mean, and sample variance are not independent [10]. Regression based asymptotic principle was developed by Neyman and it is recognized as C(α ) test [1]. Yet, we provide, in this article, an alternative and simple version to the C(α ) test and it can be exercised to check the validity of the null hypothesis H0 :β = ∞(which personifies that there has been no finite restriction on the corona incidence rate) against the alternative hypothesis, : (which refers that there is a finite and significant restriction on the corona incidence). In other words, the null hypothesis is rejected, when the test statistic 
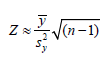is significantly larger and contradictory to Ha β < ∞.
To read more about this article......Open access Journal of Biostatistics & Biometric Applications
Please follow the URL to access more information about this article
https://irispublishers.com/abba/fulltext/an-untangling-of-global-corona-pandemics.ID.000580.php
To know more about our Journals...Iris Publishers
No comments:
Post a Comment